Projektbeschreibung

Ein breites Spektrum von mathematischen Problemen in den Ingenieurs-, Umwelt-, Finanz-, Medizin-, Physik- und anderen angewandten Wissenschaften beschäftigt sich mit der Bestimmung von sogenannten "Interfaces und/oder freien Rändern". So ist man etwa in der Bruchmechanik am Kontaktverhalten gegenüberliegender Rissflächen interessiert, um Strukturfehler zu studieren und zu erkennen; in der Finanzmathematik möchte man zur Ausübung von Optionen den Rand der Menge bestimmen, für welche der Wert einer Option gleich der Differenz aus vereinbartem Preis und aktuellem Preis eines Wertes ist; in der Medizin ist die schnelle Segmentierung von Magnetresonanzbildern von Tumoren in der intraoperativen Neuauswertung der Tumorlokalisierung von Bedeutung.

Weiter gibt es eine Vielzahl von Anwendungen, in welchen man ein System so steuern möchte, dass der Zustand - und somit der freie Rand - ein vorgegebenes Kriterium erfüllt. Beispiele für die eben erwähnte Problemstellung sind: die Rekonstruktion der Spalthöhe zwischen zwei rotierenden Flächen anhand von Messungen des Drucks in einem Schmiermittel (etwa in Gleitlagern, um ein Berühren der Flächen und somit möglichen Schaden für die Apparate zu verhindern); oder, in der Finanzmathematik, die Schätzung (und mögliche Vorhersage) der Volatilität eines Wertes anhand verfügbarer Marktdaten. Aus Sicht der Optimierungstheorie gehören diese Probleme zur Klasse der Minimierungsprobleme mit Gleichgewichtsnebenbedingungen (engl. Abkürzung MPECs für "Mathematical Programs with Equilibrium Constraints"). Aufgrund von fehlenden Regularitätseigenschaften der Nebenbedingungen, der Problemgröße und der involvierten kombinatorischen Aspekte stellen sowohl die analytische wie auch die numerische Behandlung dieser Problemklasse große Herausforderungen dar.

Diese weite Spanne von anscheinend unzusammenhängenden Problemen basiert auf einigen gemeinsamen Strukturen, was eine Formulierung in vereinheitlichten Klassen gestattet. 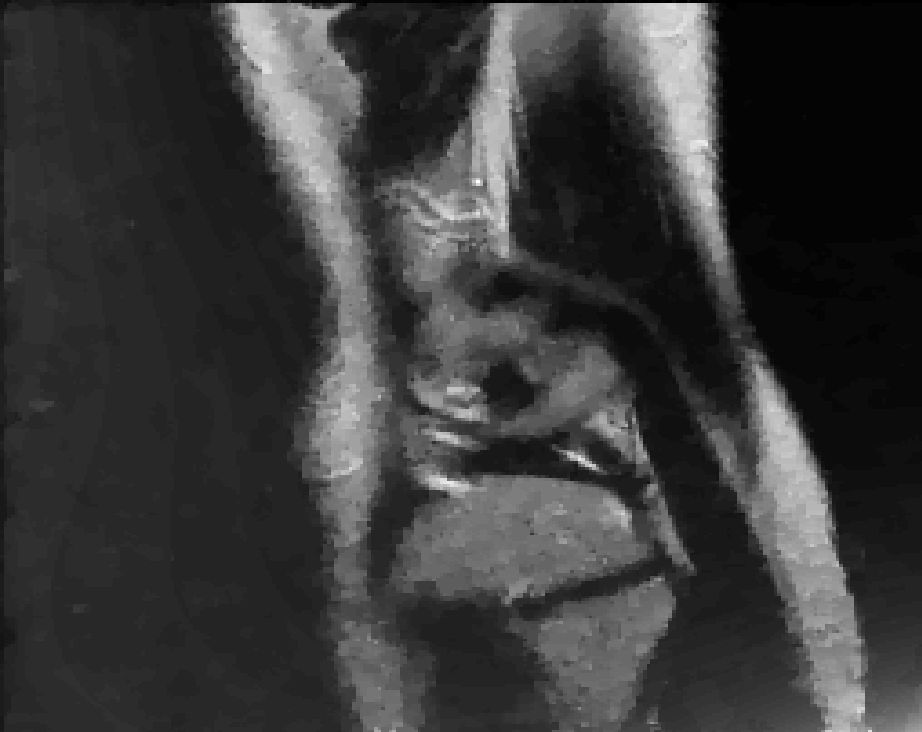Ein Beispiel: (Quasi) Variationsungleichungen bilden ein fundamentales Paradigma im Kontext der freien Randwertprobleme. Unter hinreichenden Glattheitseigenschaften kann man diese Probleme als Systeme von (im klassischen Sinne) nichtdifferenzierbaren Operatorgleichungen in Funktionenräumen auffassen. Basierend auf bisherigen Resultaten des Projektleiters und Preisträgers des vom FWF gestifteten START-Preises besteht ein Ziel dieses START-Projekts darin, das Verständnis der Theorie der verallgemeinerten Differenzierbarkeit und der verallgemeinerten Newton-Verfahren zur effizienten Lösung solcher Systeme voranzutreiben.

In manchen Fällen kann diese Reformulierung in vereinheitlichte Klassen aufgrund niedriger Regularität sogenannter Lagrange-Multiplikatoren, welche Sensitivitätsmaße bezüglich der vorhandenen (Ungleichungs-) Restriktionen sind, fehlschlagen. In anderen Situationen wiederum kann es sein, dass das reformulierte System nicht verallgemeinert differenzierbar ist. Ein Paradigmenwechsel hin zur Reformulierung der (Quasi)Variationsungleichung als Form- bzw. Topologieoptimierungsproblem anstatt als nichtdifferenzierbare Operatorgleichungen bietet eine neue Sichtweise, in welcher die Regularitätsprobleme vermieden werden können. Nun ist man an der Entwicklung schneller Lösungsverfahren für solche geometrische Optimierungsprobleme interessiert. Diese Entwicklung steht ebenfalls im Zentrum des vorliegenden Projekts. Klarerweise können diese numerischen Methoden auch auf Form- bzw. Topologieoptimierungsprobleme 'per se' angewandt werden. In diesem Sinne wird auch die Lösung von entsprechenden Problemen in der (medizinischen) Bildverarbeitung verfolgt.

Obwohl MPECs in Funktionenräumen von großer Bedeutung in den Anwendungen sind und einen Bezug zu (Quasi)Variationsungleichungen aufweisen, sind diese aus Sicht der Optimierungstheorie überraschend wenig untersucht. Auch die aktuell vorhandene Algorithmik ist bei weitem nicht zufriedenstellend. Die Projektarbeit hat hier zum Ziel, im Funktionenraum Optimalitätsbedingungen erster und zweiter Ordnung herzuleiten. In weiterer Folge dienen diese Optimalitätscharakterisierungen der Entwicklung effizienter Lösungsverfahren, welche sich wiederum auf verallgemeinerte Newton-Techniken stützen.

Eine kurze Präsentation der Forschungsschwerpunkte des START-Projekts kann hier heruntergeladen werden.