homepage/en/numerics/FJMT.2024/index.md

layout	lang	subtitle	math
default	en	FJMT.2024 / 23 April 2024	true

Lancichinetti-Fortunato-Radicchi (N_mfl = 301)

{% assign sigma_array = "0.001, 0.004, 0.012" | split: ", " %} {% assign mu_array = "0.001, 0.005, 0.01, 0.05, 0.5" | split: ", " %} {% assign prefix = "https://gaspard.janko.fr/s/numerics/FJMT.2024/plots_23_04_2024/results/LFR_single_graph/N_micro=1000,N_mfl=301" %}

This page shows the differences in the dynamics between the microscopic and the kinetic (meanfield) model for Lancichinetti-Fortunato-Radicchi (LFR) type graphs, depending on two parameters:

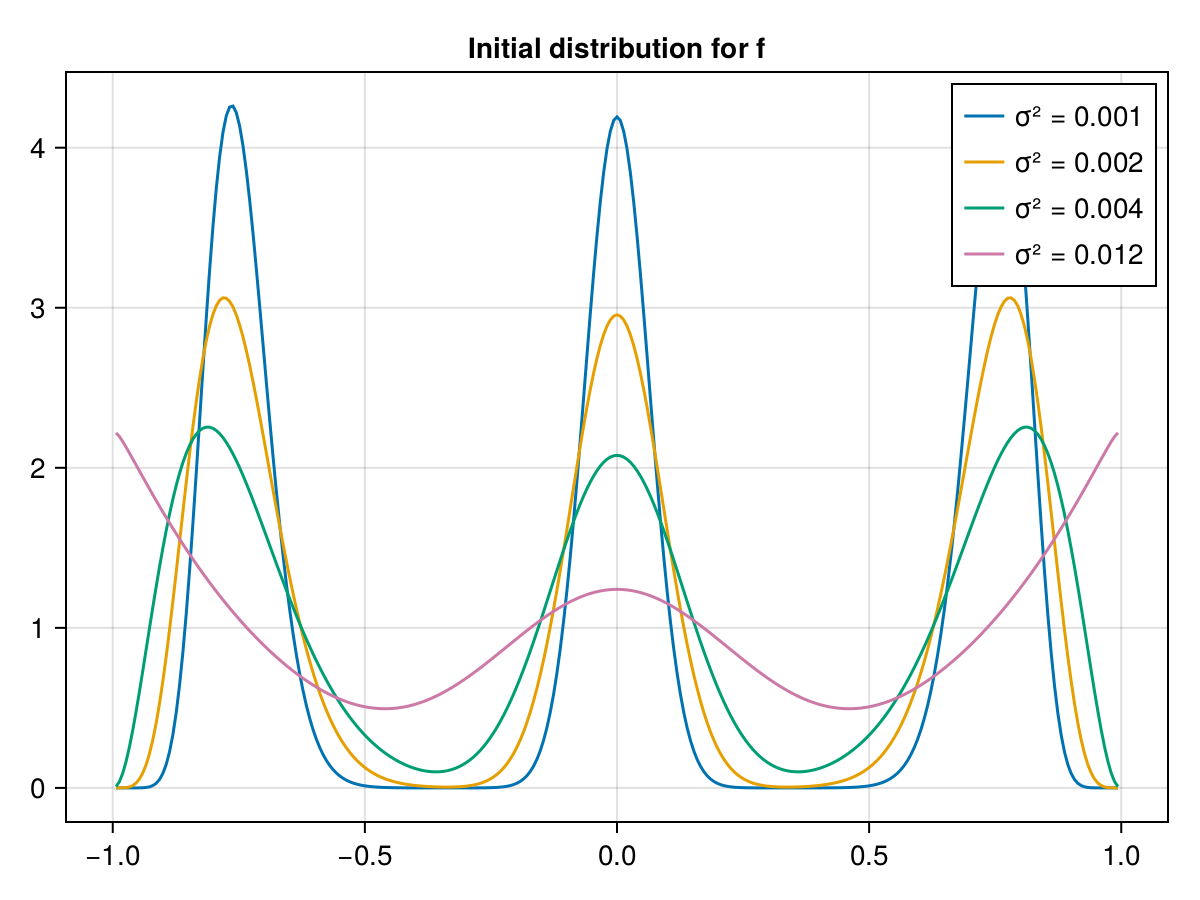
• \sigma^2, which is the variance of the \beta distributions making up the initial distribution f,
• \mu, the so-called mixing parameter for the construction of the LFR graphs.

{:width="750"}

Graphs

|----------| | {% for mu in mu_array -%} | [μ={{ mu | round: 4 }}]({{ prefix }}/reference/μ={{ mu }}/graph_LFR.png){% if forloop.last -%} | {% endif -%} {% endfor %}

{% for sigma in sigma_array %}

$β$ distribution with $σ² = {{sigma}}$

Movies (ensemble averages)

|----------| {% for mu in mu_array -%} | μ={{ mu | round: 4 }}{% if forloop.last -%} | {% endif -%}

{% endfor %}
{% for mu in mu_array -%}
[plain $w_i$]({{ prefix }}/σ²={{ sigma }}/μ={{ mu }}/movie_without_g.mp4){% if forloop.last -%}
{% endfor %}
{% for mu in mu_array -%}
[centered $w_i$]({{ prefix }}/σ²={{ sigma }}/μ={{ mu }}/movie_without_g.mp4){% if forloop.last -%}
{% endfor %}
{:.headerline.center}

Dynamics

Convergence rates are computed over the time span marked in blue in the first plot.

Parameters:

• \mu: LFR mixing parameter
• T^*: time to consensus = -1/\log(\vert\lambda_2\vert) \cdot \delta t, where \lambda_2 is the second largest eigenvalue of the transition matrix for the associated time discrete model. See here.
• assortativity
• clustering coeff.

{:.manual_center_1500}

Graph properties

{:.manual_center_1500}

g(t=0), 1 row per run, p increasing →

Brightness: 1 Invert

{:.manual_center_510}

{% endfor %}