Research
Existence and regularity of reaction-diffusion systems
Reaction-diffusion systems appear frequently in modelling a large of realistic systems, yet even the basic quesitons such as global existence of (suitable concept of) solutions and their regularity could be challenging. Of importance and interest are systems which have nonlinearities being quasi-positive (P) and conserve/dissipate the total mass (M). It was shown recently that these two natural assumptions are not enough to rule out blow-up solutions in finite time, even for polynomial nonlinearities. Yet the modelling keeps bringing such systems, especially higher order chemical reaction networks. Our research in this direction looks for other natural structures of those chemical/biological/ecological/etc systems which guarantee global existence and boundedness. On the other hand, it could shed light on how one should model e.g. a high order chemical reaction systems in the sense of diffusion, i.e. diagonal or cross-diffusion. |
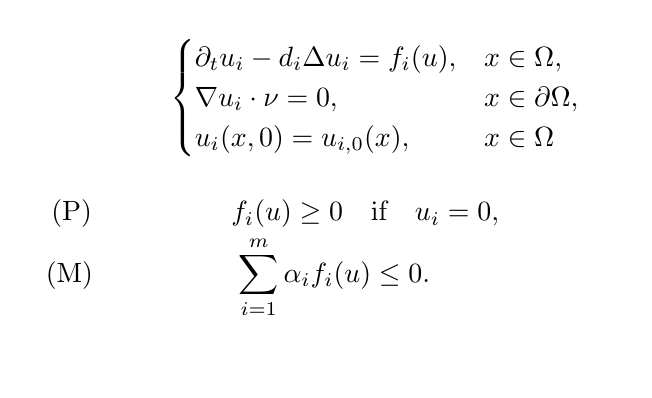 |
|---|
Entropy method and convergence to equilibrium
|
|
Equilibration and stability of equilibria are of the most desired properties of any systems. Though experiments usually confirm these properties, proving them mathematically, both qualitatively or quantatively, is usually a challenging task. A common approach is to linearise around an equilibrium and study the corresponding linearised problem to obtain local (asymptotic) stability. The entropy method is a novel fully nonlinear alternative which not only proves global stability but also provides quantitative, and in many case, optimal, convergence rates and constants. Because of that, the entropy method, which was initiated in kinetic theory, has shown in wide applicability in many other problems and its close connections to other branches such as functional inequalities, hypocoerivity or harmonic analysis. Our research utilised this entropy method in the context of chemical reaction-diffusion systems, i.e. chemical systems in the presence of diffusion. The obtained results here have surprising applications in molecular communication (see below). |
|---|
Molecular communications
The notion of MC for synthetic or artificial devices was first given in 2005. Its core idea is utilising chemical signals, like natural biological systems, to allow nanomachines to communicate where communication by means of electromagnetic or acoustic wave is impossible. Possible signigicant applications, such as future medical treatments using nanobots or targeted drug delivery, have motivated an exciting research area in the last decade. Explicitly understanding the quantitative behaviour of RDS, which model complex biological systems, plays an essential role in designing reliable algorithms for modulation and detection. Yet the question of how to constructively use these results in MC has been barely touched. In a recent work, a novel communication scheme called equilibrium signaling was proposed based on the explicit equilibration analysis of chemical RDS. The challenging issue of stochasticity in diffusion and reactions (sometimes called molecuar noise) in communication channels was addressed by approximating RDS using chemical reaction-diffusion master equations (RDME), a microscopic stochastic description of chemical reactions with diffusion. Our research in this direct establishes the mathematical foundation for the rigorous bridging between the two scales, towards rigorous design of molecular detection scheme. |
|
|---|
Stabilisation by boundary noise for PDE
|
|
Having a stable system, adding random noise might make it unstable. This is also intuitive and demonstates that noise can destabilise the system. Interestingly, the opposite direction, that is adding noise stabilises an unstable system, can also happen. This counter-intuitive phenomenon has been first observed in the seventies and investigated extensively for the finite dimensional setting, e.g. for differential systems. The situation for partial differential equations is more subtle, especially when the noise appears only on the boundary of the domain. Our recent research shows that this stabilisation by boundary noise has very interesting characteristics which make it significantly different from the case of domain noise. For instance, numerical simulations suggest that when the deterministic system is "too unstable", it is impossible to stabilise it using boundary noise. |
|---|
Attractors for deterministic/random dynamical systems from PDE
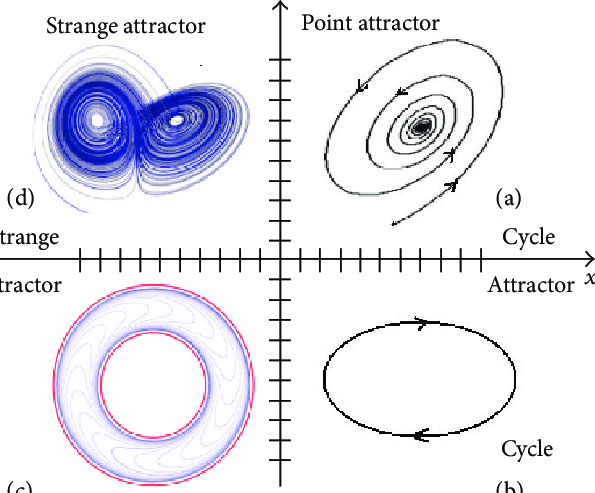
Capturing large time dynamics of infinite dimensional dynamical systems is particularly challenging to due their rich and complex behaviour. The theory of attractors was introduced in the eighties to tackle this issue. Attractors are minimal compact sets which are invariant under the flow and attracting all trajectories as time tends to infinity. In many cases, these attractors can be shown to have finite Hausdorff/fractal dimensions, which means the large time asymptotic of the system can be described using finite number of freedoms. Our research in this direction has shown existence, regularity, upper semicontinuity of attractors for various models. |
 |
|---|
