Scope

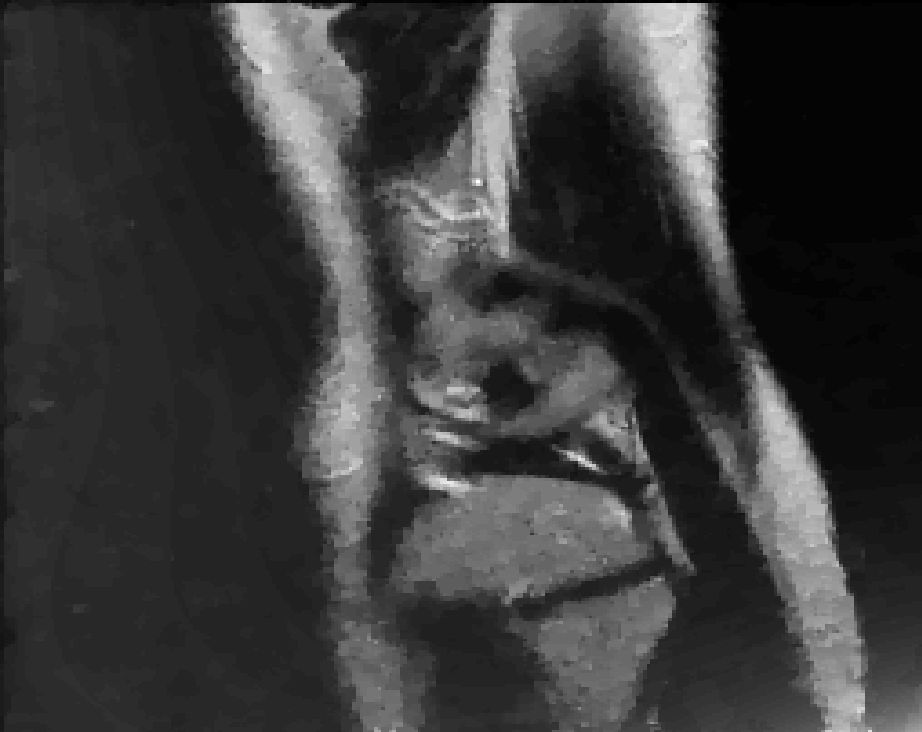
A broad spectrum of mathematical problems in engineering, environmental, financial, life, physical and other applied sciences involves the determination of so-called "interfaces and/or free boundaries". For example, in fracture mechanics, one is interested in the contact behavior of opposite crack faces to study failure of structures; in mathematical finance, one wants to compute the boundary of the set where the value of a (put) option equals the payoff (i.e., the maximum of zero and the difference of the agreed price and the price per share of the underlying asset) in order to compute the price for exercising an option; in life sciences the rapid segmentation of magnetic resonance images (MRIs) of tumors is essential for the intraoperative reassessment of tumor locations.

Further, in a number of applications one is interested in directing a process such that the state of the underlying system - and hence the corresponding free-boundary - meets a pre-specified criterion, or else one has to recover the free-boundary from measurements of some quantity. Examples for the latter types of processes are: recovering the height of a gap between two rotating surfaces by measuring the pressure of a lubricant filling this gap in order to avoid that the surfaces touch and, thus, devices potentially suffer damage; or, in finance mathematics, estimating (and possibly predicting) the volatility of an asset from available market data. From an optimization-theoretic perspective, these problems belongs to the class of so-called "mathematical programs with equilibrium constraints" (short MPECs). Due to the lack of constraint regularity, the analytical as well as the numerical treatment is challenging.

This wide range of seemingly unconnected applications is based on a few common mathematical structures, which allows rearranging these problems in unified abstract classes. For instance, a fundamental paradigm in the context of free-boundary problems is given by (quasi)variational inequalities in either a stationary or transient regime. Under sufficient smoothness assumptions, these problems can be reformulated as systems of non-differentiable equations in function space. One aim of this research project is to advance the theory of generalized differentiability and generalized Newton methods for such non-smooth systems.

In some cases, this reformulation may fail due to lack of regularity of so-called Lagrange multipliers,which are sensitivity measures of the existent inequality restrictions, or the reformulated system is not generally differentiable. A change of paradigms allows defining these problems as shape, respectively topology optimization problems which avoids regularity difficulties. In this context, the development of fast shape and topology optimization algorithms is also essential and forms another core of this project. These methods will also be applied to interface problems 'per se', such as image segmentation problems.

Although MPECs in function space are connected to important applications and are related to (quasi)variational inequalities, optimization-theoretic investigations in function space are relatively scarce and unsatisfactory from an algorithmic point of view. In this field, the aim is to establish a first and second order optimality theory for MPECs in function space and to develop and analyze efficient algorithms.

A short presentation of the START-project's research areas can be downloaded here.