1.3.5 Lokaler Datenaustausch

Das Einheitsquadrat [0, 1]² wird gleichmäßig zeilenweise in procx x procy Rechtecke 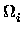$\Omega_{i}^{}$ unterteilt. Die Prozeßnummer (rank) stimmt mit der Teilgebietsnummer überein.

Abbildung A.1: Gebietsaufteilung und lokale Richtungen

Die Funktion

IniGeom(myid,procx,procy,neigh,color)

aus example/src/accuc ( example/src/accuf) generiert entsprechend obiger Gebietsaufteilung die topologischen Informationen, welche im Integerfeld neigh(4) gespeichert werden. Durch color wird eine Red-Black-Einfärbung der Prozesse definiert. Die Funktion

IniCoord(myid,procx,procy,xl,xr,yb,yt)

generiert die Koordinaten der unteren linken Ecke (xl, yb) und der oberen rechten Ecke (xr, yt) jedes Teilgebietes.

Realisiere einen lokalen Datenaustausch einer Double-Precision-Zahl zwischen jedem Prozessor und dessen (über eine gemeinsame Kante verbundenen) Nachbarn. Benutze die Funktion ExchangeD aus E8.

Jedes Teilgebiet 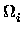$\Omega_{i}^{}$ sei wiederum gleichmäßig in (nx - 1) * (ny - 1) Rechtecke unterteilt, welche ein Dreiecksnetz beinhalten (nx, ny seien für alle Teilgebiete gleich!).
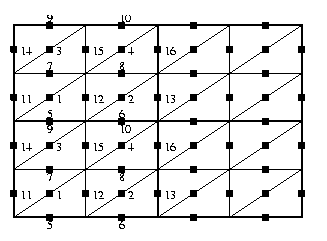
Jeder Mittelpunkt (Knoten) einer Dreieckskante entspricht 2 Komponenten eines Vektors, z.B., der Geschwindigkeit einer Flüssigkeit in diesem Punkt. Somit haben wir

• 2*(nx - 1)*(ny - 1) Unbekannte auf der Diagonalen
• 2*(nx - 1)*ny Unbekannte auf den horizontalen Linien
• 2*nx*(ny - 1) Unbekannte auf den vertikalen Linien,

d.h., nd : = 2*(3*nx*ny - 2*nx - 2*ny + 1) lokale Unbekannte pro Teilgebiet. Wir benutzen eine spezielle Numerierung, welche zeilenweise mit den Werten auf der Diagonalen beginnt, gefolgt von den horizontalen Linien und schließlich den vertikalen Linien. Die Funktion

GetBound(id,nx,ny,w,s)

kopiert die dem Rand South(id=1), East (id=2), North (id=3), West (id=4) entsprechenden Werte des Vektor w in den Hilfsvektor s. Umgekehrt addiert die Funktion

AddBound(id,nx,ny,w,s)

die Werte in s auf die entsprechenden Komponenten von w. Diese Funktion kann zur Akkumulation von Daten auf den Teilgebietsrändern benutzt werden, was eine typische Operation in parallelen Programmen ist.

Schreibe eine Funktion, welche einen verteilten Vektor  ${\ensuremath{\color{green}{\sf w}}}$ (Double Precision) (S. 82) akkumuliert. Die Rufzeile könnte folgendermaßen aussehen

VecAccu(nx,ny,w,neigh,color,myid,icomm),

wobei w sowohl Eingabe- als auch Ausgabeparameter ist.