Nächste Seite: 2. Einige Internetadressen
Aufwärts: 1.3 Die Praktikumsaufgaben
Vorherige Seite: 1.3.5 Lokaler Datenaustausch
Wir betrachten das Stokesproblem in schwacher Formulierung
(Variationsformulierung).
Finde
(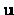 , p)
, p) 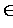
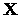 x
x 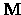 : =
: = 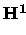 (
(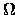 ) x L2
) x L2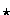 (
(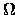 ) sodaß
) sodaß
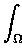 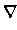  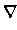 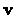 dx - dx - 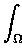 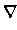 . . 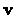 p dx p dx |
= |
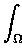 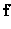 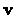 dx dx 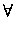 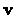 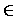 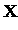 |
|
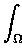 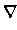 . .  q dx q dx |
= |
0 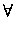 q q 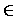 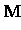 , , |
|
in
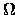 : = (0, 1)2 gilt, mit den Randbedingungen
: = (0, 1)2 gilt, mit den Randbedingungen
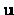 = (1, 0)T für y = 1 und
= (1, 0)T für y = 1 und
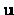 = 0 sonst auf
= 0 sonst auf
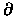
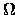 .
Die (
.
Die (
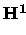 (
(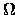 )) nichtkonformen P1-P0
Elemente sind eine stabile Diskretisierung dieses Problems.
Damit erhalten wir das Sattelpunktproblem (Formel (7.7) auf Seite 134)
Mit gegebenen Vorkonditionierern
)) nichtkonformen P1-P0
Elemente sind eine stabile Diskretisierung dieses Problems.
Damit erhalten wir das Sattelpunktproblem (Formel (7.7) auf Seite 134)
Mit gegebenen Vorkonditionierern
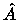 für A und
für A und 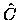 für
- BTA-1B
kann das Sattelpunktproblem mittels des vorkonditionierten
Arrow-Hurwicz Algorithmus (S. 135) gelöst werden.
für
- BTA-1B
kann das Sattelpunktproblem mittels des vorkonditionierten
Arrow-Hurwicz Algorithmus (S. 135) gelöst werden.
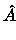 ( (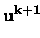 - - 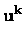 ) ) |
= |
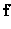 - A - A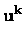 - Bpk - Bpk |
|
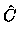 (pk + 1 - pk) (pk + 1 - pk) |
= |
BT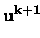 |
|
Eine serielle Programmversion ist in seqc ( seqf) zu finden.
Sie benutzt cg-Iterationen mit Diagonalskalierung für 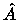 und
und
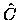 : = M, wobei
M die Massenmatrix (Gramsche Matrix) bzgl. des Druckes p darstellt.
Die Matrizen
A, B,
: = M, wobei
M die Massenmatrix (Gramsche Matrix) bzgl. des Druckes p darstellt.
Die Matrizen
A, B,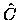 werden in
werden in
GetGradMatrix(nx, ny, 0, 0, A, id, ik)
GetDivMatrix(nx, ny, 0, 1, B, idb, ikb)
GetMassMatrix(nx, ny, 1, 1, M)
generiert. Die Diagonale von A erhält man aus
AccuDiag(nx, ny, sk, id, d)
Der Vektor der rechten Seite wird mit
GetRhs(nx, ny, f, 0, 1, 0, 1) ,
GetRhsPressure(nx, ny, g, 0, 1, 0, 1)
initialisiert. Randbedingungen werden mittels
DirichletBc(nx, ny, A, id, ik, f, u)
eingebaut und die Anfangslösung wird mit
SetU(nx, ny, u, 0, 1, 0, 1)
initialisiert.
Die Operationen
w : = w + 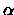 Au,
p : = p +
Au,
p : = p + 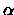 BTu,
u : = u +
BTu,
u : = u + 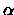 Bp sind implementiert in
Bp sind implementiert in
CrsMult(1, nu, w, u, id, ik, A, 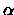 )
)
BTCrsMult(np, nu, p, u, idb, ikb, B , 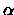 )
)
BCrsMult(np, nu, p, u, idb, ikb, B, 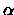 )
) .

- Leite aus dem sequentiellen Code eine parallele Version ab!



Nächste Seite: 2. Einige Internetadressen
Aufwärts: 1.3 Die Praktikumsaufgaben
Vorherige Seite: 1.3.5 Lokaler Datenaustausch
Gundolf Haase
1999-10-04
![]() , p)
, p) ![]()
![]() x
x ![]() : =
: = ![]() (
(![]() ) x L2
) x L2![]() (
(![]() ) sodaß
) sodaß