

Next: About this document ...
Up: Course on Parallelization
Previous: 5 Local data exchange
Subsections
As model problem, we consider the homogeneous Dirichlet boundary value problem
(
u(x) = 0 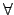 x
x 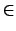
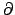
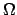 )
for the Poisson equation in the unit square
)
for the Poisson equation in the unit square
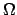 : = (0, 1)2
in its weak formulation:
: = (0, 1)2
in its weak formulation:
Find
u 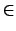 H10(
H10(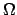 ) such that
) such that
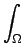 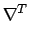 u(x) u(x)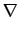 v(x) dx = v(x) dx = 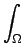 f(x)v(x) dx f(x)v(x) dx 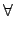 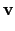 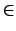 H10( H10(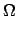 ) . ) . |
(1) |
We use linear finite elements for the discretization and achieve the linear system
of equations
K . 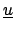 = = 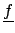 . . |
(2) |
Let us denote the diagonal of matrix K by
D = diag(K).
Now, we can formulate the 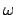 -Jacobi iteration
-Jacobi iteration
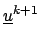 = = 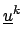 + + 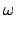 . D-1 . ( . D-1 . (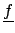 - K . - K . 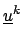 ) , k = 0, 1, 2,... . ) , k = 0, 1, 2,... . |
(3) |
You will find a sequential version of the Jacobi solver in the directory
Solution/jacseqc with the following functions in addition to the functions
from P 5.
in which matrix K and right hand side
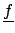 are calculated using
the function
FunctF(x,y)
for describing
are calculated using
the function
FunctF(x,y)
for describing
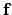 (x).
Note, that only coordinates and element connectivities are
related to the rectangular domain - all other parts in this routine are
written for general 2d-domains.
(x).
Note, that only coordinates and element connectivities are
related to the rectangular domain - all other parts in this routine are
written for general 2d-domains.
The Dirichlet boundary conditions are
set in
SetU(nx, ny, u).
Alternatively, one could use FunctU(x,y).
These b.c. are applied in
via penalty method.
The solver itself is implemented in
and uses
to get the diagonal from matrix K.
Matrix-times-vector is realized in
A vector
 can be saved in file named name by calling
can be saved in file named name by calling
such that
gnuplot jac.dem
will give an impression of that vector.
-

- Implement a parallel version of the sequential code !
Here, we will solve (2) by means of a multigrid iteration.
You will find a sequential version of the multigrid solver using
a 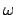 -Jacobi iterations a smoother and, for simplicity, also as a
coarse grid solver
in the directory
Solution/mgseqc .
The following functions are added to the functions
from previous sections.
-Jacobi iterations a smoother and, for simplicity, also as a
coarse grid solver
in the directory
Solution/mgseqc .
The following functions are added to the functions
from previous sections.
AllocLevels(nlevels, nx, ny, pp, ierr)
allocates the memory for all levels and stores the pointers in
variable pp which is a structure PointerStruct. For details
see
mg.h .
The matrices and right hand sides will
be calculated in
FreeLevels(nlevels, pp, ierr)
frees the allocated memory at the end.
Note, that we need for multigrid a different procedure to apply the
Dirichlet b.c.
The multigrid solver
uses crtl as predefined structure ControlStruct to control the
multigrid cycle (mg.h).
The same holds for each mg-iteration
MGM(pp, crtl, level, neigh) .
The mg components smoothing, coarse grid solver, interpolation and
restriction are defined in
A vector
 on level level can be saved in file named name
by calling
on level level can be saved in file named name
by calling
SaveVector(name, pp->u[level], pp->nx[level],
pp->ny[level],
u, nx, ny, xl, xr, yb, yt, ierr) ,
such that
gnuplot mgm.dem
will give an impression of that vector.
-

- Implement a parallel version of the sequential code !


Next: About this document ...
Up: Course on Parallelization
Previous: 5 Local data exchange
Gundolf Haase
2003-05-19
![]() H10(
H10(![]() ) such that
) such that