5 Local data exchange

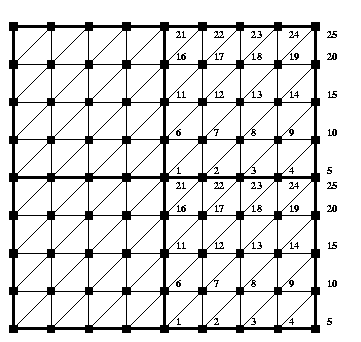
Let the unit square [0, 1]² be partitioned uniformly into procx x procy rectangles $\Omega_{i}^{}$ numbered row by row. The numbering of the subdomains coincides with the corresponding process-id's (ranks).

The function

IniGeom(myid,procx,procy,neigh,color)

from example/accuc (example/accuf) generates the topological relations corresponding to the domain decomposition defined above. These information are stored in the integer array neigh(4). A check-board coloring is defined in color. Moreover, the function

IniCoord(myid,procx,procy,xl,xr,yb,yt)

can be used to generate the coordinates of the lower left corner (xl, yb) and the upper right corner (xr, yt) of each subdomain.

Realize a local data exchange of a double precision number between each processor and all of it's neighbors (connected by a common edge). Use the routine ExchangeD from E8.

Let each subdomain $\Omega_{i}^{}$ be uniformly discretized into nx * ny rectangles generating a triangular mesh (nx, ny are the same for all subdomains !).
If we use linear f.e. test functions then each vertex the triangles represents one component of the solution vector, e.g., the temperatur in this point, and we have nd : = (nx + 1) * (ny + 1) local unknowns within one subdomain. We propose a locally rowise ordering of the unknowns.
Note, that the global number of unknowns is N = (procx*nx + 1) * (procy*ny + 1) < procx*procy*nd ) .

GetBound(id,nx,ny,w,s)

copies the values of w corresponding to the boundary South(id=1), East (id=2), North (id=3), West (id=4) into the auxiliary vector s. Vice versa, the function

AddBound(id,nx,ny,w,s)

adds the values of s to the components of w corresponding to the nodes on the boundary South(id=1), East (id=2), North (id=3), West (id=4). These functions can be used for the accumulation (summation) of values corresponding to the nodes on the interfaces between two adjacent subdomains which is a typical and necessary operation.

Write a routine which accumulates a distributed Double Precision vector w. The call of such a routine could look as follows

VecAccu(nx,ny,w,neigh,color,myid,icomm)

where w is both in- and output vector.