Sub-Optimal Control of Transient Non-Isothermal Viscoelastic Fluid Flows

Non-Newtonians fluids, among them viscoelastic fluids, exhibit some remarkable phenomena, which is due to their "elastic" nature. These fluids keep memory of their past deformations, and their behaviour is a function of these old deformations. Examples of viscoelastic fluids are oil, liquid polymers, glycerine etc. Computer simulations have become an important tool for the ingeneering of polymer processing. These simulations offer the means to optimize polymers processes such as injection molding and extrusion for example. The injection molding process can be modelled by simulating the flow of a viscoelastic fluid in a contracting channel (the 4-to-1 contracting channel is a benchmark problem in viscoelastic fluid flows simulations). During the industrial process, defaults usually occur. One of the reason is the presence of vortices in the corners of the contraction, see Fig 1. This phenomenon does not occur for Newtonians fluids at the same Reynods numbers.
We wish to control viscoelastic fluids in order to remove these vortices. As thermal effect are well known for their impact on viscoelastic fluid flows, we decide that the control mechanism will be based on heating or cooling the fluid along a portion of the flow domain. Nevertheless, models taking into account the heat tranfert can be quite complicated. Therefore we utilize a simplified model : the parameters of the fluid (viscosity and relaxation time) are set depending on the temperature following the so-called WLF model, and the heat transfer is modelled with the usual heat equation. Finally four coupled equations are needed to model the flow of non-isothermal viscoelastic fluids : the momentum equation, the mass balance, a constitutive equation relating the stress tensor to the deformation tensor, and the heat transfer equation.

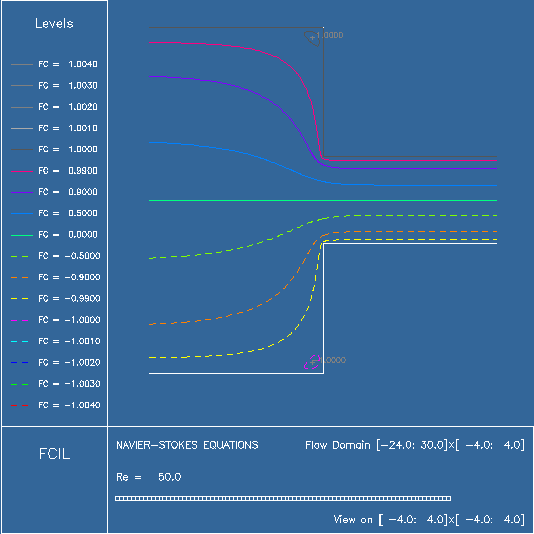
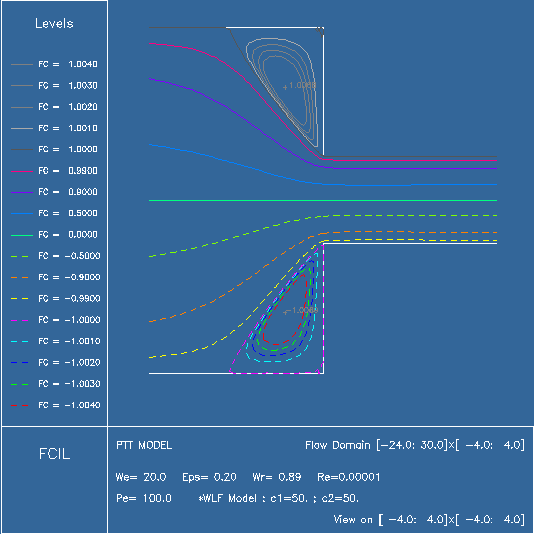
As we consider transient flows, optimal control strategies can be unfeasible on account of the size of the system of governing equations. Therefore sub-optimal strategies are required. We decide to utilize the so-called "instantaneous control" strategy. Instantaneous control is based on time discretization of an evolutionnary set of equations with optimal control problem being solved at each time instance. Although the strategy violates the Bellmann principle and the HJB appraoch, it can be effective in the sence of control design, and be justified as a receding horizon technique.

To eliminate the vortices in the flow, we minimize a cost functional depending on the flow parameters and expressing the presence of vortices. An efficient cost functional turns out to be:
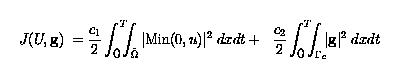
where U is the velocity field in the flow domain (U = (u,v)), g, the control, is the temperature at the boundary of the domain and [0,T] is the time interval on which we control the fluid. Minimizing J implies that regions with vortices are penalized. (Note that the choice of the "best" cost functional is not a trivial task). Also J utilizes two design parameters c1 and c2 corresponding to the relative cost of the penalty term and the control.

To minimize J, an optimality system using Lagrange multipliers is derived. The instantaneous control strategy implies minimizing Jn at each time instance, where Jn is the equivalent of J, but at one time tn.
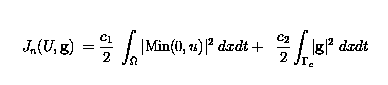
Results of the simulations showing the evolution with respect to time of the streamlines of the flow, the heat inside the flow domain, the control at the boundary and the cost functional can be found here.
References:
  • K. Kunisch, X. Marduel, Optimal Control of Non-Isothermal Viscoelastic Fluid Flows
    18.8 mB postscript file
    6.3 mB pdf file
  • X. Marduel, K. Kunisch, Sub-Optimal Control of Transient Non-Isothermal Viscoelastic Fluid Flows
    1.3 mB postscript file
    670 kB pdf file
last changed: 6/23/2003