A basic exam template for Typst, typesetting available in German and English.
https://imsc.uni-graz.at/git/gjankowiak/typst-exam/
- Typst 100%
| lib.typ | ||
| README.md | ||
| screenshot-example.png | ||
| typst.toml | ||
The exam package
This is a simple package to typeset exams. With it, you can define exercises, and items, each with a number of points. A summary is then printed on the front page.
Installation (Linux only)
Using typship
typship download -n local https://imsc.uni-graz.at/git/gjankowiak/typst-exam/
Manually
mkdir -p ~/.local/share/typst/packages/local/exam
cd ~/.local/share/typst/packages/local/exam
curl https://imsc.uni-graz.at/git/gjankowiak/typst-exam/archive/v0.1.0.tar.gz | tar zx --xform 's/typst-exam/0.1.0/'
Usage
Writing an exam is now easy:
#import "@local/exam:0.1.0": exam, exercise_header, exercise_items, mtext
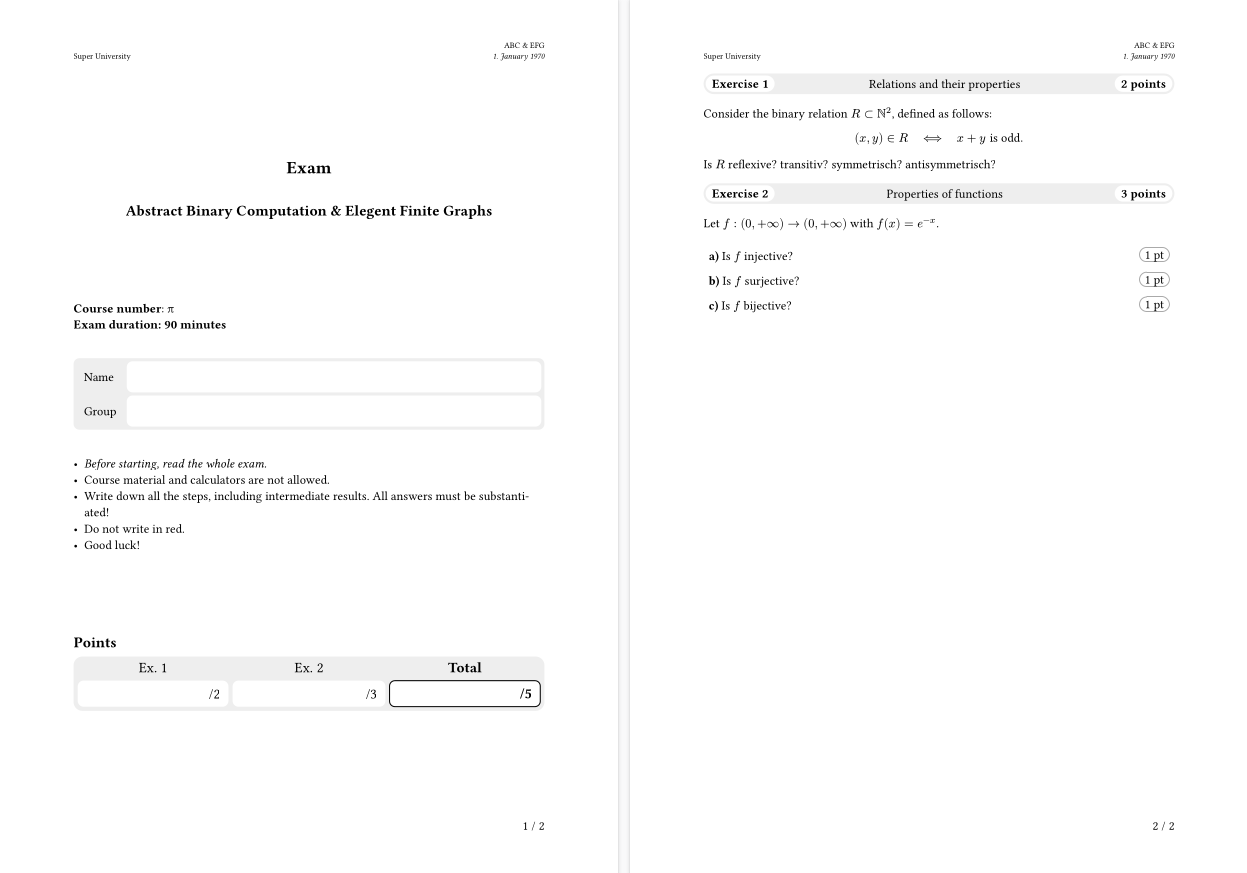
#show: exam.with(
title: "Exam",
course_title: [Abstract Binary Computation & Elegent Finite Graphs],
institution: [Super University],
date: "1. January 1970",
course_short_title: "ABC & EFG",
course_number: "π",
duration_minutes: "90",
ask_trainer_name: false,
ask_group: true,
language: "en",
)
Defining exercises and items
A new exercise can be started using #exercise_header("title", nb_points), for example:
#exercise_header("Relations and their properties", 2)
Consider the relation $R subset NN^2$, defined as follows:
$ (x, y) in R #h(0.5cm) <==> #h(0.5cm) x + y #mtext[is odd]. $
Is $R$ reflexive? transitiv? symmetrisch? antisymmetrisch?
On can also defined (sub-)items for the exercise using #exercise_items(items, override_points:true),
where items is an array of (nb_points, statement). By default, the number of points the exercise
is worth is recomputed as the sum of points for all items. This behaviour can be turned off by
setting override_points: false.
#exercise_header("Properties of functions", 3)
Let $f : (0, +infinity) → (0, +infinity)$ with $f (x) = e^(-x)$.
#exercise_items((
(1, [Is $f$ injective?]),
(1, [Is $f$ surjective?]),
(1, [Is $f$ bijective?]),
))
All together, this should output something like:
Utilities
mtext(str)to typeset text within math mode using the default text font.frame(stroke_width)providesstrokefor use in atable, horizontal lines only, top and bottom lines are bold.