Scope
State of the art
The numerical treatment of parameter identification problems for
partial differential equations (PDEs) arising in diverse areas of
science and (industrial or economic) applications has received an
increasing amount of attention in the recent past. In many situations these problems can be
formulated as optimal control problems for PDEs. For the optimization of systems governed by PDEs, second-order algorithms, such as
Newton or sequential quadratic programming (SQP) methods have been
developed and analyzed in detail. The augmented Lagrange-SQP method and its inexact variant - including globalization strategies - was analyzed by scientists of the University of Graz, for instance.
Parameter estimation of engineering components or systems often
requires repeated, reliable, and real-time prediction of the
parameters such as forces, critical stresses, flow rates or heat
fluxes. In recent publications, efficient optimization methods such as the augmented Lagrange-SQP method have been combined with a model reduction based on proper orthogonal decomposition (POD). POD
is a method for deriving low order models for systems of
differential equations. It is based on projecting the system onto
subspaces consisting of basis elements that contain characteristics
of the expected solution. The POD basis in parabolic problems is derived from
solutions to the underlying PDE for different time-instances. In applications where we face
elliptic parameter-dependent systems, the POD basis is derived from
solutions to the underlying PDE for different parameter values.
Generally, we will concentrate on problems to estimate
parameters μ in a parameter space 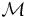 ⊂
⊂
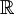 m, m
m, m 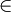
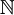 , from measurements ud for either the solution
u=u(μ), μ
, from measurements ud for either the solution
u=u(μ), μ 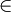
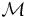 , to the elliptic variational
problem
, to the elliptic variational
problem
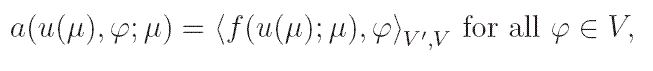
where V is an appropriate Hilbert space with dual V',
a( · , · ;μ): V × V → 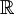 denotes a bilinear
form depending on the parameter μ
denotes a bilinear
form depending on the parameter μ 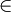
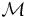 and f( · ;μ): V → V'
is a non-linear mapping, which may depend also on the parameter μ
and f( · ;μ): V → V'
is a non-linear mapping, which may depend also on the parameter μ
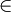
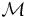 , or for the solution
u=u(t,μ), (t,μ)
, or for the solution
u=u(t,μ), (t,μ) 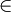 [0,T] ×
[0,T] × 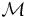 , to the
parabolic variational problem
, to the
parabolic variational problem
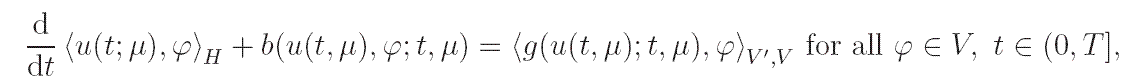
where H ⊂ V is a Hilbert space that is dense in V,
b( · , · ;t,μ): V × V → 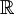 denotes a
bilinear form and g( · ;t,μ): V → V' is a non-linear
mapping both depending on the time t
denotes a
bilinear form and g( · ;t,μ): V → V' is a non-linear
mapping both depending on the time t 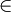 [0,T] and on the
parameter μ
[0,T] and on the
parameter μ 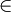
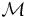 .
.
In applications, the parameters, that have to be identified,
typically satisfy certain inequality constraints. For instance, the
parameters are bounded from below and above for physical or
technical reasons. Hence, we suppose that the parameter set
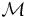 ⊂
⊂ 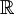 m has the form
m has the form
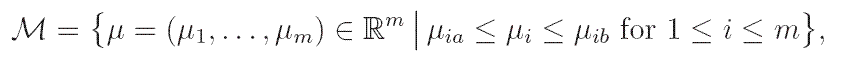
where μia and μib denote lower and upper bounds,
respectively, for the i-th component of the parameter μ 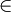
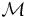 .
.
The resulting parameter estimation problem can be written as a constrained optimal control problem.
Aims of the project
The main focus of the project is the
development of efficient reliable solution methods for constrained
parameter estimation problems governed by a class of elliptic as
well as parabolic non-linear PDEs, where the parameters are scalars
or constants on subdomains.
The POD method is compared to other model reduction methods, such as reduced-basis element methods or balanced truncation,
and we plan to use these methods within our algorithm.
We also aim to apply our technique on an example arising in (industrial) applications. In the development of modern
vehicles efficient and precise prediction techniques are needed for
the vehicle interior noise. The steady-state sound pressure p satisfies the Helmholtz equation, which depends
non-linearly on the frequency parameter.
While the sound pressure is measurable utilizing technical devices, the
involved parameters can often
not be measured directly. Therefore, parameter identification
problems governed by the Helmholtz equation are important and
interesting in (industrial) applications. We aim to study POD
Galerkin approximations for the Helmholtz equation and utilize these
approximations within this (non-linear) parameter estimation problem.
We will carry out error analysis for the discretized problems and discuss issues like choice of snapshots or topology for the POD basis computation.
First steps are already done for scalar parameters. These results have to be
extended to several parameters or for parameters which are constant
on subdomains. Moreover, non-linear dependence on the parameters is
an interesting issue. This is, e.g., the case for the Helmholtz
equation.
Furthermore, a-posteriori analysis can be carried
out for the POD solution by solving a additional adjoint problem. In a cooperation
with Prof. F. Tröltzsch (Berlin University of Technology) we plan
to incorporate a-posteriori POD error analysis in the POD solver.
As optimization methods we aim to use augmented Lagrange
algorithms combined with globalized SQP or Newton methods or
semi-smooth Newton variants. Since the augmented Lagrange SQP method has already been investigated in this context in previous papers,
we will concentrate on semi-smooth Newton methods, which
turn out to be very efficient for box constrained optimal control problems, for example.
It was shown that the
active set strategy is equivalent to a semi-smooth Newton method
and, as a consequence, that it converges at a locally
superlinear rate. Since Hessian information is utilized, the
semi-smooth Newton method is a second-order method. Second-order
information typically speeds up the convergence locally near a
solution of the optimal control problem satisfying second-order
sufficient optimality conditions.
The designed algorithms are tested with
respect to global convergence, rate of convergence and efficiency.
In the parameter estimation for hyperthermia problems on-line strategies are needed to control the individual medical treatment
of a patient during an application.
We aim to provide a POD discretization to on-line parameter estimation problems arising in
hyperthermia that can be used for fast and reliable computations in a cooperation
with Dr. Weiser from the Zuse Institute Berlin.
In our project we will also focus on time-dependent problems. Scalar parameters in the linear and non-linear heat
equation are estimated. Here we aim to utilize the semi-smooth
Newton method.
Moreover, we plan to extend our error analysis to parameter estimation
problems that can be written as linear-quadratic optimal control
problems. The work shall be also influenced by the cooperation with Prof. Dr. M. Hinze from the University of Hamburg.
The solution methods which we will develop in our project will be implemented and tested in MATLAB utilizing the FEMLAB package for
the finite element discretization.
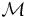 ⊂
⊂
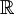 m, m
m, m 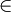
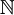 , from measurements ud for either the solution
u=u(μ), μ
, from measurements ud for either the solution
u=u(μ), μ 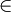
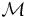 , to the elliptic variational
problem
, to the elliptic variational
problem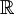 denotes a bilinear
form depending on the parameter μ
denotes a bilinear
form depending on the parameter μ 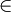
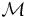 and f( · ;μ): V → V'
is a non-linear mapping, which may depend also on the parameter μ
and f( · ;μ): V → V'
is a non-linear mapping, which may depend also on the parameter μ
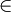
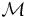 , or for the solution
u=u(t,μ), (t,μ)
, or for the solution
u=u(t,μ), (t,μ) 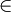 [0,T] ×
[0,T] × 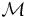 , to the
parabolic variational problem
, to the
parabolic variational problem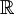 denotes a
bilinear form and g( · ;t,μ): V → V' is a non-linear
mapping both depending on the time t
denotes a
bilinear form and g( · ;t,μ): V → V' is a non-linear
mapping both depending on the time t 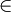 [0,T] and on the
parameter μ
[0,T] and on the
parameter μ 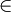
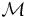 .
.
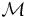 ⊂
⊂ 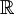 m has the form
m has the form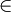
 .
.