Parameter Estimation in Variational Inequalities
This project is concerned with the identification of a (positive) distributed parameter u in variational inequalities of the type
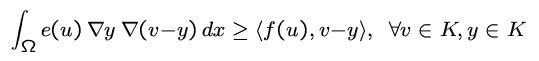
where ![]() and
and![]() suitaby chosen.
suitaby chosen.
Introducing a non-negative slack variable (multiplier)![]() the variational inequality is equivalent to
the variational inequality is equivalent to
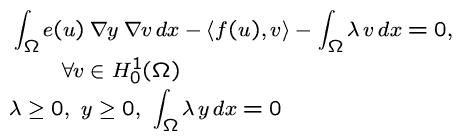
This system is also called equilibrium system.
Identification problems for variational inequalities frequently occur in practical applications. For instance, the estimation of the height function u between two rotating surfaces in elastohydrodynamic lubrication problems belongs to the present problem class. In this situatuation the variational inequality stems from the Reynolds lubrication equation and the additional requirement that the pressure y is nonnegative.
A common technique to identify the parameter u from measurements z of y is based on a regularized least squares formulation

Note that the (model) variational inequality is the necessary and sufficient first order condition for the lower level minimization problem in the above least squares problem. The characterization of an optimal solution (y*,u*) of the above bilevel optimization problem is usually based on multipliers. If we replace the lower level minimization problem by its optimality system, i.e. the equilibrium system from above, as a so called equilibrium constraint, then existence of multipliers may fail even in practically relevant situations.
?Typical results on existence of multipliers available from the literature either guarantee multipliers in very general situations but are not amenable for numerical realization, or the corresponding first order conditions are numerically implementable but existence of multipliers fails in specific important cases.
Our aim is to derive multipliers that exist in general
and,
the corresponding first order characterization is immediately amenable for numerical realization.
This is achived by the following strategy:
- Primal-dual penalization: This strategy applies to the lower level problem, i.e. the explicit constraint is replaced by an implicit one. The resulting new (unconstrained) lower level problem is
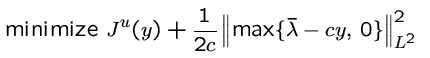
where c>0 denotes a penalty parameter. - Complementarity functions: This technique allows to replace the complementarity system with a single equality, i.e.
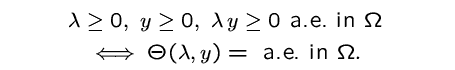
The optimal solution (u*,y*,l*) of the regularized least squares problem with corresponding multipliers (p*,m*) is characterized by the following first order necessary optimality conditions:
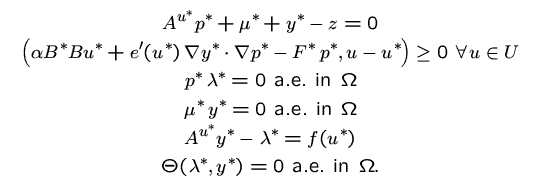
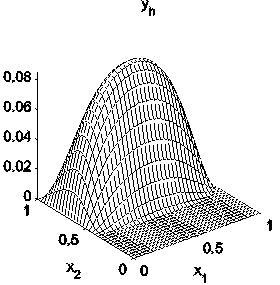
Numerical result for the lubrication problem
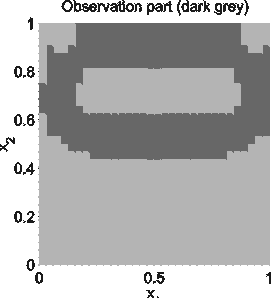
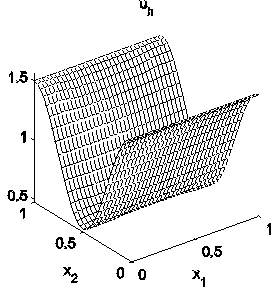
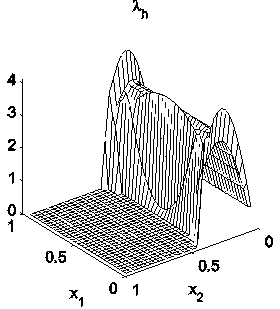
The numerical realization is based on a finite element discretization of the above first order necessary conditions. The pointwise conditions are enforced at the nodes of the discretization. The resulting nonlinear system is solved by a stabilized Gauss-Newton method combined with an interior technique for u. The latter approach allows to rewrite the variational inequality in the first order system as an equality. The identification is done on a suitable observation set (see the figure below). The graphs below show the observation part of the domain and the respective reconstructions.
 |
 |
|
 |
||
 |