Identification of the load of a partially breaking
beam from inclination measurements
Engineering Background
Steel-concrete piles are frequently used to protect steep mountain slopes against landslides (see the graphic below). We consider the problem of finding the load acting on a pile from measurements of its deformation. With u denoting the displacement of the pile with respect to its vertical axis we assume that we are given measurements of the inclination u' along the length of the pile. Thus, we are given a typical inverse problem where we have knowledge of the solution of a differential equation (the Euler beam equation in our case) and we want to estimate a quantity which occurs as a parameter in the differential equation.
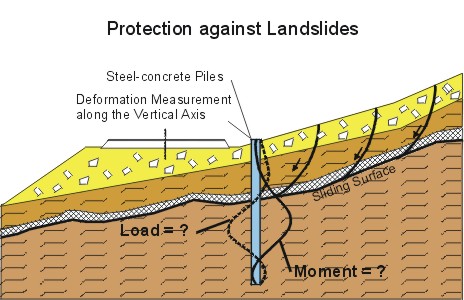
Discontinuous Constitutive Relation
We assume that the relation between the known u' and the unknown moment m is discontinuous due to partial breaking of the steel-concrete pile at the tensile side if the moment exceeds a critical value. If we formulate the problem as a constrained least-squares problem, the partial breaking yields a non-smooth, non-convex equality constraint.
Two-Step Solution Strategy
We pursue the following two-step strategy to solve the inverse problem:
- Identify the broken and unbroken parts of the beam. It is seen that the broken and unbroken parts are separated by jump discontinuities in the curvature of the beam. The curvature function is estimated by solving a regularized least-squares problem. Here the regularization term is of total variation type. Total variation regularization is especially suitable to resolve discontinuities.
- By assigning appropriate material constants to the broken and unbroken parts, we only need to solve a linear inverse problem to find the load p and the moment m.
Numerical Results
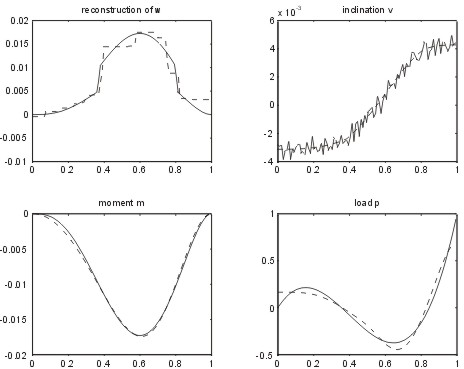
The plot shows the results of the estimation of the curvature function w (upper left), the noisy data u' (upper right), the recon-struction of the moment m (lower left) and the load p (lower right). Note that the jump discontinuities in w are resolved quite well by the total variation regularization approach.
Research is done in cooperation with Dr. Roman Marte, Institut für Grundbau und Bodenmechanik, Technische Universität Graz.
Reference:
- W. Ring, Identification of the Load of a Partially Breaking Beam, Inverse Problems, 15 (4) 1999.