Ziege-Weide Aufgabe
https://de.wikipedia.org/wiki/Ziegenproblem_(Geometrie) (meine Loesung schaut aehnlich aus)
Das symbolischen Paket von Matlab wird benutzt so weit es geht und zum Schluss muss numerisch geloest werden.
Contents
Variablen
symbolisch (gesuchte Groessen)
clc; clear all; %clf; % syms l real positive; l = sym('l','positive'); % Leinenlaenge % syms x real positive; x = sym('x','positive'); % x-wert des Schnittpunktes Wiesenkreis mit Leinenkreis % gegebene Groessen, hier als Zahlenwert R = 10; % Wiesenradius assumeAlso(l<2*R);
Die beiden Kurven (symbolisch)
yR = R - sqrt(R^2-x^2); yL = sqrt(l^2-x^2);
bestimme den Schnittpunkt
X = solve(yL - yR, x); % Ausgabe disp('Schnittpunkt der beiden Kurven') pretty(yR); pretty(yL) disp('ist') pretty(X)
Schnittpunkt der beiden Kurven
2
10 - sqrt(100 - x )
2 2
sqrt(l - x )
ist
/ (l - 20) (l + 20) \
l sqrt| - ----------------- |
\ 100 /
-----------------------------
2
unbestimmtes Integrieren
I = int(yL - yR, x);
Einsetzen der Integrationsgrenzen
==> abgegraste Flaeche, symbolische Funktion A(l)
A = 2*int(yL - yR, x, 0,X); % Ausgabe disp('abgegrasten Flaeche, Funktion A(l)') pretty(A)
abgegrasten Flaeche, Funktion A(l)
3
/ l #1 \ l #1 2
asin| ---- | 100 + ----- - 10 l #1 + l
\ 20 / 40
/ 4 \
| l 2 |
l #1 sqrt| --- - l + 100 |
/ #1 \ \ 400 /
asin| -- | + ---------------------------
\ 2 / 2
where
/ 2 \
| l |
#1 == sqrt| 4 - --- |
\ 100 /
Aufstellen der Gleichung, sodass die halbe Flaeche abgegrast wurde
Hier konvertieren wir eine symbolische Funktion in eine numerische Funktion.
Fs= A - pi*R^2/2; % symbolische Funktion F = matlabFunction(Fs); % numerische Funktion % Grafik % xx=linspace(0,2*R,1001); % plot(xx,F(xx),[xx(1) xx(end)],[0 0 ],'b') % title('A(L)-pi*R^2/2'); xlabel('L') fplot(Fs,[0,2*R]) hold on plot([0,2*R],[0 0 ],'b') hold off stringFs=strjoin(arrayfun(@char, Fs, 'uniform', 0)); title('Area = A(L)-pi*R^2/2'); xlabel('L')
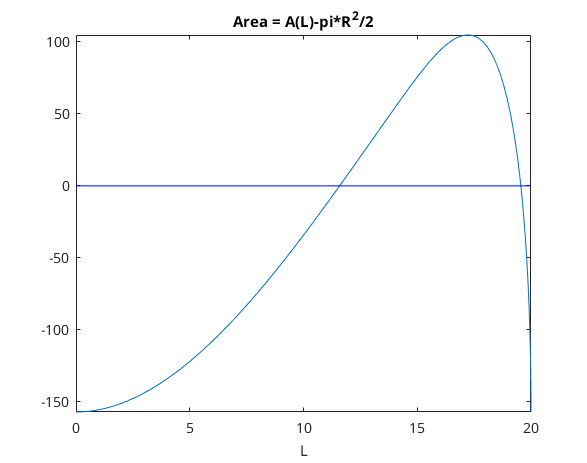
numerisches Bestimmen der Nullstelle (= Loesung)
Hier wird nicht exakt gelöst !!
options = optimset('Display','iter'); L = fzero(F, R, options) % only with optimization package %options = optimoptions(@fsolve,'Display','iter') % Wie geht das genau? % options = optimoptions(optimoptions(fsolve),'Display','iter') % L = fsolve(F,R)
Search for an interval around 10 containing a sign change:
Func-count a f(a) b f(b) Procedure
1 10 -34.2427 10 -34.2427 initial interval
3 9.71716 -40.1279 10.2828 -28.2823 search
5 9.6 -42.5422 10.4 -25.7928 search
7 9.43431 -45.932 10.5657 -22.2528 search
9 9.2 -50.6744 10.8 -17.2101 search
11 8.86863 -57.2728 11.1314 -10.0123 search
13 8.4 -66.3711 11.6 0.280816 search
Search for a zero in the interval [8.4, 11.6]:
Func-count x f(x) Procedure
13 11.6 0.280816 initial
14 11.5865 -0.0169335 interpolation
15 11.5873 -2.35373e-06 interpolation
16 11.5873 3.90799e-14 interpolation
17 11.5873 3.90799e-14 interpolation
Zero found in the interval [8.4, 11.6]
L =
11.5873
Grafik
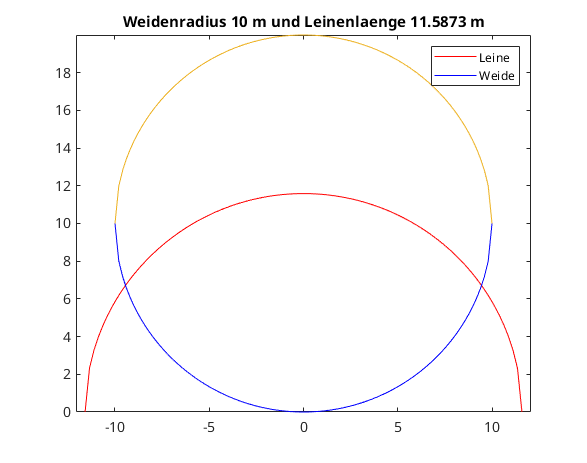
n = 100; % Leinenkurve xxL = linspace(-L, L, n); yyL = subs(subs(yL,l,L),x,xxL); % Wiesenkurve xxR = linspace(-R, R, n); yyR = subs(yR,xxR); plot(xxL,yyL,'r'); hold on; plot(xxR,yyR,'b'); plot(xxR,2*R-yyR); plot(xxL,R); axis equal title(['Weidenradius ',num2str(R),' m und Leinenlaenge ',num2str(L),' m']); legend('Leine','Weide'); % publish('ziege_wiese.m');