Contents

CompMath-Vorlesung

Wiederholung FOR-Zyklus Einfuehrung in die strukturierte Programmierung: WHILE, DO_WHILE Umwandlung FOR-Zyklus in WHILE-Zyklus

clc; clear;
disp(datetime)

   31-Oct-2025 17:16:37

FOR-Zyklus: Produkt ungerader Zahlen <= n

n = 10;
p =  1;
for k=1:2:n
    p = p*k;
end
disp(['Produkt ungerader Zahlen bis n = ', num2str(n),' : ',num2str( p )])
disp(['Produkt ungerader Zahlen bis n = ', num2str(n),' : ',num2str( prod(1:2:n) )])

Produkt ungerader Zahlen bis n = 10 : 945
Produkt ungerader Zahlen bis n = 10 : 945

FOR-Zyklus: Fibonacci-Zahlen

F(1) = F(2) = 1;  F(k) = F(k-1)+F(k-2)  fuer k>=3

clc; clear;
n = 10;
F(1) = 1;
F(2) = 2;
for k=3:n
    F(k) = F(k-1)+F(k-2);
end
disp("Fibonacci: "+num2str(F))

Fibonacci: 1   2   3   5   8  13  21  34  55  89

abweisender Zyklus [WHILE-Loop]

Ziel: Eingabe einer durch 7 teilbaren Zahl

clc; clear;
disp('abweisender Zyklus')
count = 0;      % Zaehlt die Zyklendurchlaufe
% k = input("durch 7 teilbare Zahl: ");
k = 1;          % Erzwingt mindestens einen Durchlauf des nachfolgenden Zyklus, da Test False ergibt
while  mod(k,7) ~= 0
%     k = input("durch 7 teilbare Zahl: ");
    k = randi([-7,95],1);
    count = count+1;
end
k
disp("#Versuche: "+count);

abweisender Zyklus

k =

    21

#Versuche: 7

abweisender Zyklus [WHILE-Loop]

Groesster gemeinsamer Teiler fuer nichtnegative ganze Zahlen a und b nach dem Euklid-Algorithmus.

clear; clc;
b_org = 17*123*2*3*7;
a_org = 17*7*13*2;

a = a_org; b = b_org;
r = mod(a,b);
while r>0
    a = b;
    b = r;
    r = mod(a,b);
end
disp("ggT von "+a_org+" und "+b_org+" ist "+b)
disp("mit Matlab-Fkt: gcd(a,b): "+gcd(a_org,b_org))

ggT von 3094 und 87822 ist 238
mit Matlab-Fkt: gcd(a,b): 238

Reihenberechnung via Vektorarithmetik (und Speicherung aller Partialsummen)

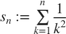
und der Wert der Reihe ist

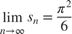
clc; clear
disp('Reihe via Vektorarithmetik')
realval = pi^2/6;         % wahrer Reihenwert
KK = 1./(1:1000).^2;      %  Folgenglieder
SS = cumsum(KK);          %  Partialsummen (oder einfach nur sum(KK) )
disp("Differenz zu pi^2/6: "+(SS(end)-realval));

Reihe via Vektorarithmetik
Differenz zu pi^2/6: -0.0009995

Reihenberechnung via Zaehlschleife

clc; clear
disp('Reihe via Zaehlschleife')
realval = pi^2/6;      % wahrer Reihenwert
sum(1) = 1;
for k=2:1000
%   Partialsumme        Folgenglied
    sum(k) = sum(k-1) + 1/k^2;
end
disp("Differenz zu pi^2/6: "+(sum(end)-realval));

Reihe via Zaehlschleife
Differenz zu pi^2/6: -0.0009995

Reihenberechnung via Zaehlzyklus in While-Zyklus umwandlen

clc; clear
disp('Zaehlschleife in While-Loop umwandlen')
realval = pi^2/6;               % wahrer Reihenwert
sum(1) = 1;
k = 2;                          % Laufvariable: Anfangswert setzen
while k<=1000                   % Laufvariable: bzgl. Endwert testen
    sum(k) = sum(k-1) + 1/k^2;
    k = k+1;                    % Laufvariable veraendern
end
disp("Differenz zu pi^2/6: "+(sum(end)-realval));

Zaehlschleife in While-Loop umwandlen
Differenz zu pi^2/6: -0.0009995

Zaehlzklus in While umwandlen mit Abbruch

clc; clear
disp('Reihe via While-Loop')
realval = pi^2/6;      % wahrer Reihenwert
seps = 1e-3;          % relative Abbruchgenauigkeit
sum(1) = 1;
k = 2;
while k<=100000 && abs(sum(k-1)-realval) >= seps
%while  abs(sum(k-1)-realval) >= seps   % absoluter Test
    sum(k) = sum(k-1) + 1/k^2;
    k = k+1;
end
disp("Differenz zu pi^2/6: "+(sum(end)-realval));
disp("N: "+length(sum));

Reihe via While-Loop
Differenz zu pi^2/6: -0.0009995
N: 1000

Zyklus mit While und unbekanntem Ergebnis

clc;

clear
disp('Reihe via While-Loop')
seps = 1e-4 ;          % relative Abbruchgenauigkeit
sum(1) = 1;
k = 2;
add_term = 10*seps;    % erster Test in WHILE soll FALSE ergeben
while  abs(add_term) >= seps   % absoluter Test mit aktuell addiertem Term
    add_term = 1/k^2;
    sum(k) = sum(k-1) + add_term;
    k = k+1;
end
disp("Differenz zu pi^2/6: "+(sum(end)-pi^2/6));
disp("N: "+length(sum));

Reihe via While-Loop
Differenz zu pi^2/6: -0.0098521
N: 101

Published with MATLAB® R2025b