Wolf-Hase: Räuber-Beute-Modell

System zweier gekoppelter ODES. Siehe auch die Lotka-Volterra-Gleichungen.

Contents

Parameter der Evolutionsgleichungen festlegen

clear; clc; clf; close all
alpha = 8.5;    % Todesrate der Woelfe
beta  = 10;     % Vermehrungsrate der Hasen
gamma = 0.01;   % Nachwuchsrate der Woelfe (dank Beute=Hasen)
delta = 0.07;   % Todesrate der Hasen (durch die Jaeger=Woelfe)

time_a = 0;     % Startzeit
time_b = 2;     % Endzeit
tau = 1/1000;    % Schrittweite in der Zeit

t  = time_a:tau:time_b;
nt = length(t); % Anzahl der Zeitschritte

Anfangspopulationen

wolf(1) = 100;
hase(1) = 1000;

Zeititeration.

Exlizites Schema der Zeitintegration. Erfordert sehr kleine Zeitschrittweite für numerische Stabilität.

wolf(nt) = 0;         % Stellt Speicher fuer alle benoetigetn Vektorelemente bereit.
hase(nt) = 0;

for m = 2:nt
    wolf(m) = wolf(m-1) -tau*alpha*wolf(m-1) + tau*gamma*wolf(m-1)*hase(m-1);
    hase(m) = hase(m-1) +tau*beta *hase(m-1) - tau*delta*wolf(m-1)*hase(m-1);
end

Ergebnisse anzeigen

% alt: mit plotyy
% [AX,H1,H2] = plotyy(t,wolf,t,hase);
% title('Räuber-Beute-Modell');
% xlabel('Zeit');
% set(H1,'LineStyle','--')
% set(H2,'Color','r')
% set(get(AX(1),'Ylabel'),'String','Wölfe')
% set(get(AX(2),'Ylabel'),'String','Hasen')
% set(get(AX(2),'Ylabel'),'Color','r')

% neu: mit yyaxis
yyaxis left
plot(t,wolf,'--b')
ylabel('Wölfe')
hold on

yyaxis right
plot(t,hase,'-r')
ylabel('Hasen')

title('Räuber-Beute-Modell: simple explizite Zeitintegration');
xlabel('Zeit');

saveas(gcf,'wolf_hase.jpg');    % Speicher die aktuelle Grafik als jpg-File
hold off

% publish('wolf_hase.m')

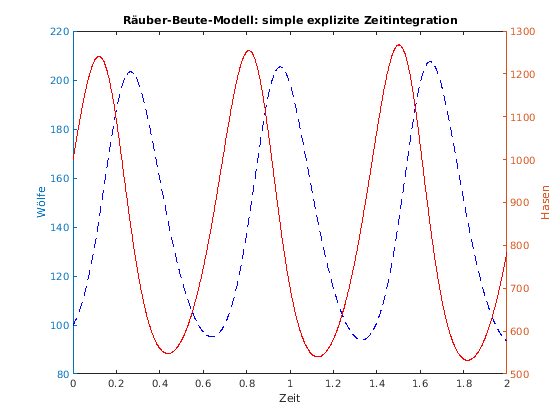
Solve as system of ODEs

figure
tspan = [time_a time_b];
y0    = [wolf(1),hase(1)];
[t,yode] = ode45(@(t,y) odefcn(t,y,alpha,beta,gamma,delta), tspan, y0);

Visualisierung

plot(t,yode) neu: mit yyaxis

yyaxis left
plot(t,yode(:,1),'--b')
ylabel('Wölfe')
hold on

yyaxis right
plot(t,yode(:,2),'-r')
ylabel('Hasen')

title('Räuber-Beute-Modell: Löser ode45');
xlabel('Zeit');

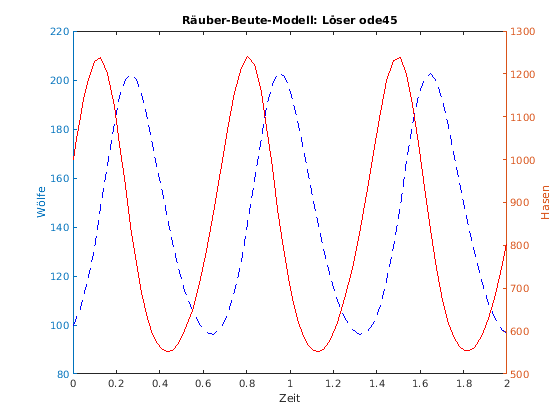
Beschreibung des ODE-Systems

$$ \frac{dw(t)}{dt} = -\alpha w(t) + \gamma w(t)h(t) \qquad\qquad \frac{dh(t)}{dt} = \beta w(t) - \delta w(t)h(t) $$

function dy = odefcn(t,y,alpha,beta,gamma,delta)
dy = zeros(2,1);
dy(1) = -alpha*y(1) + gamma*y(1)*y(2);
dy(2) =  beta *y(2) - delta*y(1)*y(2);
end


Published with MATLAB® R2019a