ADE surfaces*


$A_1$ (aka The Cone)
$x^2+y^2-z^2=0$
$A_1$ in different coordinates
$z^2+x^2-y^2=0$
$A_2$ (aka The Cusp)
$z^2+y^2+x^3=0$
$A_4$
$z^2+y^2+x^5=0$
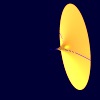
$A_6$
$z^2+y^2+x^7=0$
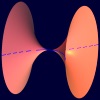
$A_3$
$z^2+y^2-x^4=0$
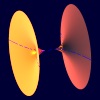
$A_5$
$z^2+y^2-x^6=0$
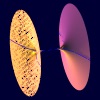
$A_7$
$z^2+y^2-x^8=0$
$D_4$
$ z^2+x(y^2-x^2)=0$
$D_6$
$ z^2+x(y^2-x^4)=0$
$D_8$
$ z^2+x(y^2-x^6)=0$
$D_5$
$ z^2+x(y^2-x^3)=0$
$D_7$
$ z^2+x(y^2-x^5)=0$
$D_9$
$ z^2+x(y^2-x^7)=0$
$E_6$
$z^2+x^3+y^4=0$
$E_7$
$z^2+x(x^2+y^3)=0$
$E_8$
$z^2+x^3+y^5=0$

*: Real pictures of some complex quotient singularities $\mathbb{C}^2 / \Gamma$, where $\Gamma$ is a finite subgroup of $SL_2(\mathbb{C})$. These surfaces are also known as ADE surfaces or Kleinian surfaces or $2$-dimensional rational double points or ...
In each surface a curve is highlighted. This curve is the intersection of the surface with the plane $\{ z =0 \}$, or, if we stay in the context of groups, it is the discriminant curve of the complex reflection group $G$ such that $[G:\Gamma]=2$, that is, $\Gamma=G \cap SL_2(\mathbb{C})$.

All pictures were produced with POV-Ray . For questions, comments, suggestions etc., please contact me .