SATV

Introduction

During acquisition and transmission, images are often blurred and corrupted by Gaussian noise. In many applications, the deblurring and denoising of such images are fundamental for subsequent image processing operations, such as edge detection, segmentation, object recognition, and many more.

In order to restore the degraded images and preserve significant details in the images, Rudin, Osher and Fatemi proposed total variation (TV) regularization. Based on this model, we consider the improved version



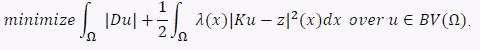
In the model, the parameter λ controls the trade-off between a good fit of z and a smoothness requirement due to the total variation regularization. Since images are, in general, comprised of multiple objects at different scales, we utilize different values of λ localized at image features of different scales in order to obtain better restoration results.

In the SA-TV method, we propose a local variance estimator in order to decide, in a robust way, on the scales of the features contained in z. Our λ-adjustment is fully automated and, thus, requires no user interaction. In order to accelerate the performance of the λ-update scheme we generalize the hierarchical decomposition approach to spatially dependent λ. The corresponding subproblems are solved by a superlinearly convergent algorithm based on Fenchel-duality and inexact semismooth Newton techniques.

(Jump to download section)

---

Results

Example 1: Restoration of Noisy Image

Example 2: Restoration of Blurred Noisy Image

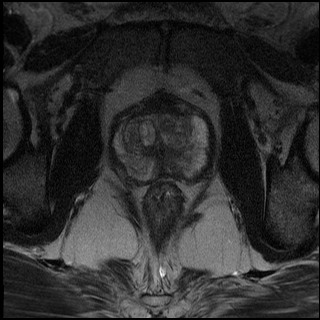
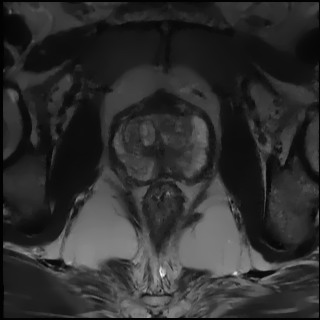
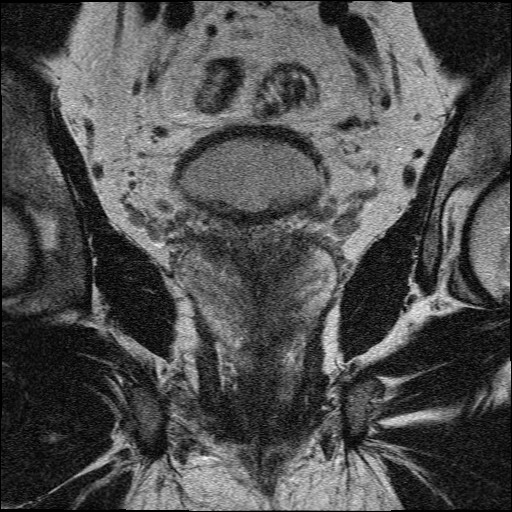
Example 3: Restoration of MRI

---

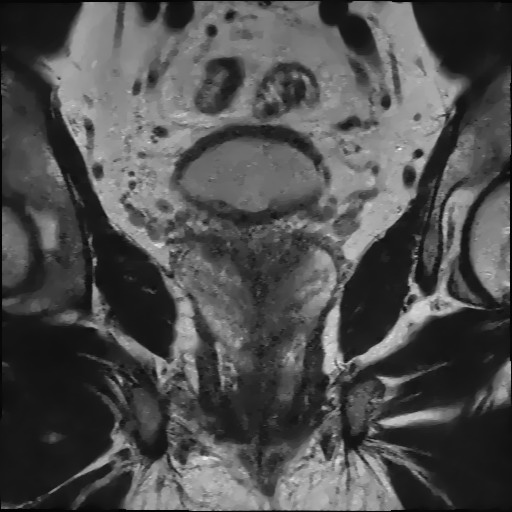
Downloads

- SA-TV Software
- Readme-File
- Slide presentation

Please observe the disclaimer information below.

---

References

- For scalar regularization parameter-based solver:

[1] M. Hintermüller and G. Stadler, "An Infeasible Primal-Dual Algorithm for Total Bounded Variation-Based Inf-Convolution-Type Image Restoration", SIAM Journal on Scientific Computing, 28(1): 1-23, 2006. View article online.

- For spatially dependent parameter-based solver:

[2] Y.Q. Dong, M. Hintermüller and M. M. Rincon-Camacho, "Automated Regularization Parameter Selection in a Multi-Scale Variation Model for Image Restoration", accepted for publication in Journal of Mathematical imaging and vision, IFB-Report No. 22 (11/2008), Institute of Mathematics and Scientific Computing, University of Graz. Download

- For color image restoration (which is not yet included in this version of the toolbox):

[3] Y.Q. Dong, M. Hintermüller and M. M. Rincon-Camacho, "A Multi- Scale Vectorial L^τ-TV Framework for Color Image Restoration", International Journal of Computer Vision. DOI: 10.1007/s11263-010-0359-1. Download

---

Disclaimer

The SATV method was developed by Y.Q. Dong, M. Hintermüller and M. M. Rincon-Camacho at the Institute of Mathematics and Scientific Computing of the University of Graz, and the Department of Mathematics of the Humboldt-University of Berlin. This work was supported by the Austria Science Fund FWF under START-program Y305 "Interfaces and Free Boundaries" (IFB) and the SFB F32 "Mathematical Optimization and Applications in Biomedical Sciences" (MOBIS).

The SATV Toolbox may be used for NON-COMMERCIAL RESEARCH purposes only. For inquiries concerning a different use, please contact Prof. M. Hintermüller at the Humboldt-University of Berlin.

Your comments are welcome. Please keep track of bugs or missing/confusing instructions and report them to

Yiqiu Dong
Michael Hintermüller
M. Monserrat Rincon-Camacho

The algorithms contained in the SATV Toolbox were implemented by Martin Kanitsar (University of Graz) and revised by Yiqiu Dong.