Contents

Ziege-Weide Aufgabe

Problemstellung und Loseung (meine Loesung schaut aehnlich aus)

Das symbolischen Paket von Matlab wird benutzt so weit es geht und zum Schluss muss numerisch geloest werden.

clc; clear all; close all
disp(datetime)

   26-Nov-2024 12:43:27

Variablen

symbolisch (gesuchte Groessen)

% syms l real positive;
l = sym('l','positive');          % Leinenlaenge
% syms x real positive;
x = sym('x','positive');          % x-wert des Schnittpunktes Wiesenkreis mit Leinenkreis
% gegebene Groessen, hier als Zahlenwert
R = sym('R','positive');          % Wiesenradius
assumeAlso(l<2*R);

Rval = 10;                        %

Die beiden Kurven (symbolisch)

yR(x,R,l) = R - sqrt(R^2-x^2);
yL(x,R,l) = sqrt(l^2-x^2);

% yR(x,y,R,l) = x^2+(y-R)^2-R^2;
% yL(x,y,R,l) = x^2+    x^2-l^2;

bestimme den Schnittpunkt

X(R,l) = solve(yL==yR, x);

% Ausgabe
disp('Schnittpunkt der beiden Kurven')
pretty(yR); pretty(yL)
disp('ist')
pretty(X)

Schnittpunkt der beiden Kurven
          2    2
R - sqrt(R  - x )

      2    2
sqrt(l  - x )

ist
l sqrt((2 R + l) (2 R - l))
---------------------------
            2 R

unbestimmtes Integrieren

I = int(yL - yR, x);
pretty(I)

 2     / x \                                              2     / x \
l  asin| - |                 2    2            2    2    R  asin| - |
       \ l /         x sqrt(R  - x )   x sqrt(l  - x )          \ R /
------------ - R x + --------------- + --------------- + ------------
      2                     2                 2                2

Einsetzen der Integrationsgrenzen im bestimmten Integral

==> abgegraste Flaeche, symbolische Funktion A(R,l)

A = 2*int(yL - yR, x, 0,X);

% Ausgabe
disp('abgegraste Flaeche, Funktion A(R,l)')
pretty(A)

abgegraste Flaeche, Funktion A(R,l)
/                    /             4  \ \
|                    |  2    2    l   | |
|         R l #1 sqrt| R  - l  + ---- | |
|  3                 |              2 | |
| l  #1              \           4 R  / |
| ----- + ----------------------------- | 2
\   8                   4               /      2     /  #1 \
------------------------------------------- + l  asin| --- | - l #1
                      2                              \ 2 R /
                     R

      2     / l #1 \
   + R  asin| ---- |
            |    2 |
            \ 2 R  /

where

                 2    2
   #1 == sqrt(4 R  - l )

Aufstellen der Gleichung, sodass die halbe Flaeche abgegrast wurde

Hier konvertieren wir eine symbolische Funktion in eine numerische Funktion.

Area_half(R,l) = A - pi*R^2/2;    % symbolische Funktion
pretty(Area_half)
F = matlabFunction(Area_half);    % numerische Funktion

% Grafik
% xx=linspace(0,2*R,1001);
% plot(xx,F(xx),[xx(1) xx(end)],[0 0 ],'b')
% title('A(L)-pi*R^2/2'); xlabel('L')

% R_vek=linspace(0.1,20,101);
fplot(Area_half(Rval,l),[0,2*Rval])
hold on
plot([0,2*Rval],[0 0 ],'b')
hold off
stringFs=strjoin(arrayfun(@char, Area_half(Rval,l), 'uniform', 0));
title('Area = A(L)-pi*R^2/2'); xlabel('L')

/                    /             4  \ \
|                    |  2    2    l   | |
|         R l #1 sqrt| R  - l  + ---- | |
|  3                 |              2 | |
| l  #1              \           4 R  / |
| ----- + ----------------------------- | 2       2
\   8                   4               /     pi R
------------------------------------------- - -----
                      2                         2
                     R

      2     /  #1 \           2     / l #1 \
   + l  asin| --- | - l #1 + R  asin| ---- |
            \ 2 R /                 |    2 |
                                    \ 2 R  /

where

                 2    2
   #1 == sqrt(4 R  - l )

numerisches Bestimmen der Nullstelle (= Loesung) (sym numbers)

L = solve( Area_half(R,l) == 0, l) % keine Lösung L = solve( Area_half(Rval,l) == 0, l) % keine Lösung

L = vpasolve( Area_half(Rval,l) == 0, l, Rval)
Lval = eval(L);

 
L =
 
11.587284730181215178282335099335
 

numerisches Bestimmen der Nullstelle (= Loesung) via fzero

% Hier wird näherungsweise gelöst !! options = optimset('Display','iter'); L_fzero = fzero(matlabFunction(Area_half(Rval,l)), Rval, options) % only with optimization package

numerisches Bestimmen der Nullstelle (= Loesung) via fsolve

% Hier wird näherungsweise gelöst !! options = optimoptions(@fsolve,'Display','iter') % Wie geht das genau? L_fsolve = fsolve(matlabFunction(Area_half(Rval,l)),Rval)

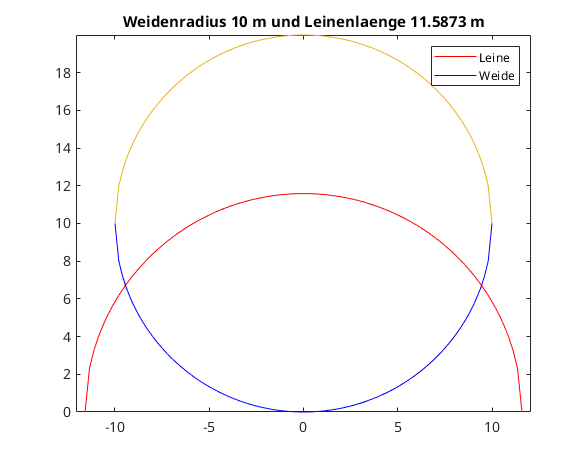
Grafik

n  = 100;
% Leinenkurve
xxL = linspace(-Lval, Lval, n);
yyL = eval(yL(xxL,Rval,Lval));
% Wiesenkurve
xxR = linspace(-Rval, Rval, n);
yyR = eval(yR(xxR,Rval,Lval));

plot(xxL,yyL,'r');              % Leinenbogen
hold on;
plot(xxR,yyR,'b');              % unterer Kreisbogen
plot(xxR,2*Rval-yyR);           % oberer Kreisbogen
plot(xxL,Rval);
axis equal
title(['Weidenradius ',num2str(Rval),' m und Leinenlaenge ',num2str(Lval),' m']);
legend('Leine','Weide');

% publish('ziege_wiese.m');

Published with MATLAB® R2024a