Contents

Wolf-Hase: Räuber-Beute-Modell

System zweier gekoppelter ODES. Siehe auch die Lotka-Volterra-Gleichungen.

clear; clc; close all
disp(datetime)

   31-Oct-2025 16:33:17

Parameter der Evolutionsgleichungen festlegen

alpha = 8.5;    % Todesrate der Woelfe
beta  = 10;     % Vermehrungsrate der Hasen
gamma = 0.01;   % Nachwuchsrate der Woelfe (dank Beute=Hasen)
delta = 0.07;   % Todesrate der Hasen (durch die Jaeger=Woelfe)


tau  = 1/1000;  % Schrittweite in der Zeit
tend = 2;       % Endzeit

Anfangspopulationen

wolf(1) = 100;
hase(1) = 1000;

Zeititeration

Anzahl der Zeitschritte

nt = tend/tau;
wolf(nt) = 0;         % Stellt Speicher fuer alle benoetigten Vektorelemente bereit.
hase(nt) = 0;

for m = 2:nt
    wolf(m) = wolf(m-1) -tau*alpha*wolf(m-1) + tau*gamma*wolf(m-1)*hase(m-1);
    hase(m) = hase(m-1) +tau*beta *hase(m-1) - tau*delta*wolf(m-1)*hase(m-1);
end

Ergebnisse anzeigen

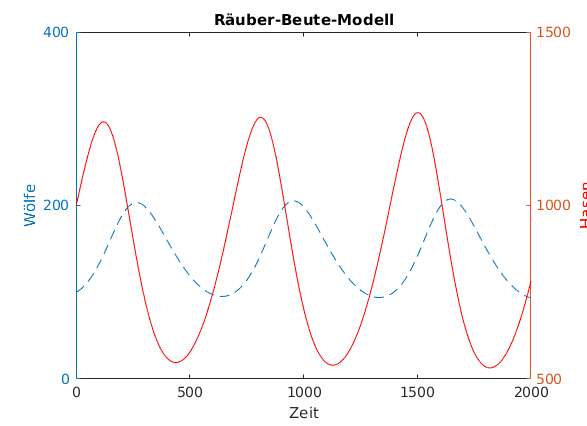
figure(1)
[AX,H1,H2] = plotyy(1:nt,wolf,1:nt,hase);
title('Räuber-Beute-Modell (numerisch)');
xlabel('Zeit');
set(H1,'LineStyle','--')
set(H2,'Color','r')
set(get(AX(1),'Ylabel'),'String','Wölfe')
set(get(AX(2),'Ylabel'),'String','Hasen')
set(get(AX(2),'Ylabel'),'Color','r')
% set(get(AX(2),'Yaxis'),'YColor','r')
% ylabel('Hasen','Color',[1 0 0]);

saveas(gcf,'wolf_hase.jpg');    % Speicher die aktuelle Grafik als jpg-File

Und jetzt über die ODEs

siehe: doc ode

figure(2)
F = ode;
F.InitialValue = [wolf(1), hase(1)];
F.ODEFcn = @(t,y) [-alpha*y(1)+gamma*y(1)*y(2);
                     beta*y(2)-delta*y(2)*y(1) ];

S=solve(F,0,tend);
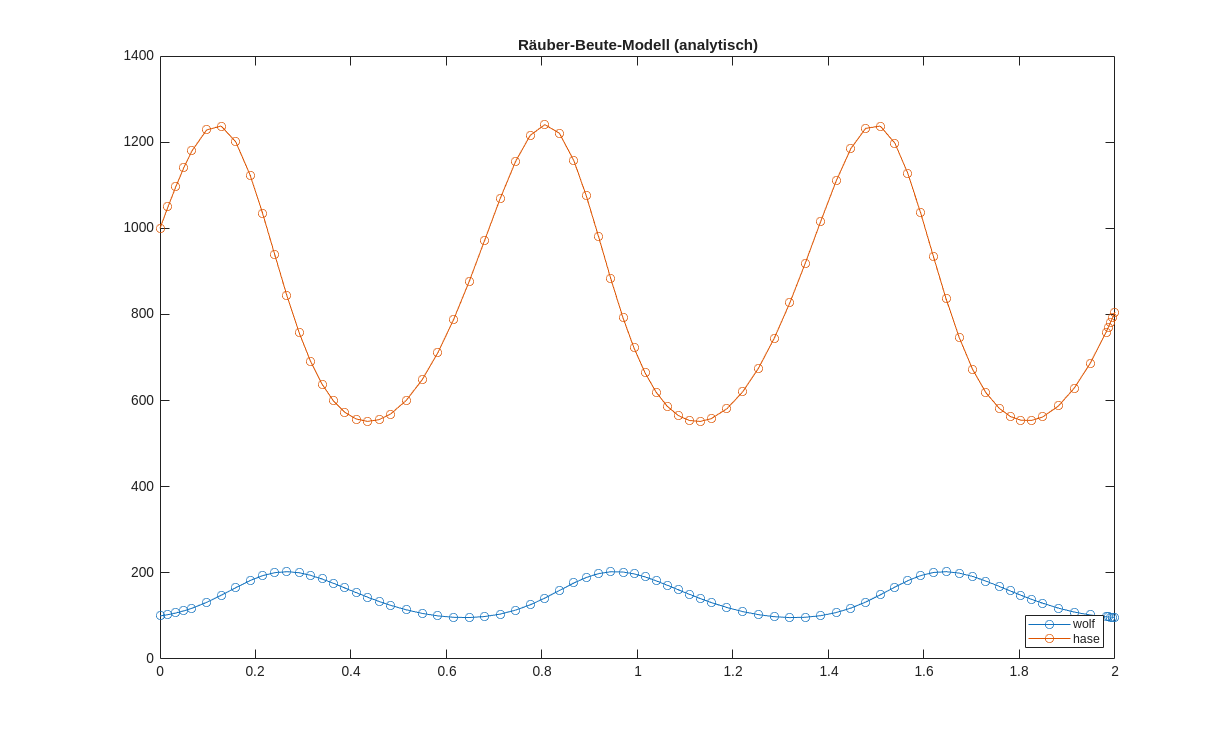
plot(S.Time,S.Solution,"-o")
title('Räuber-Beute-Modell (analytisch)');
legend("wolf","hase",Location="southeast")

saveas(gcf,'wolf_hase_ode.jpg');

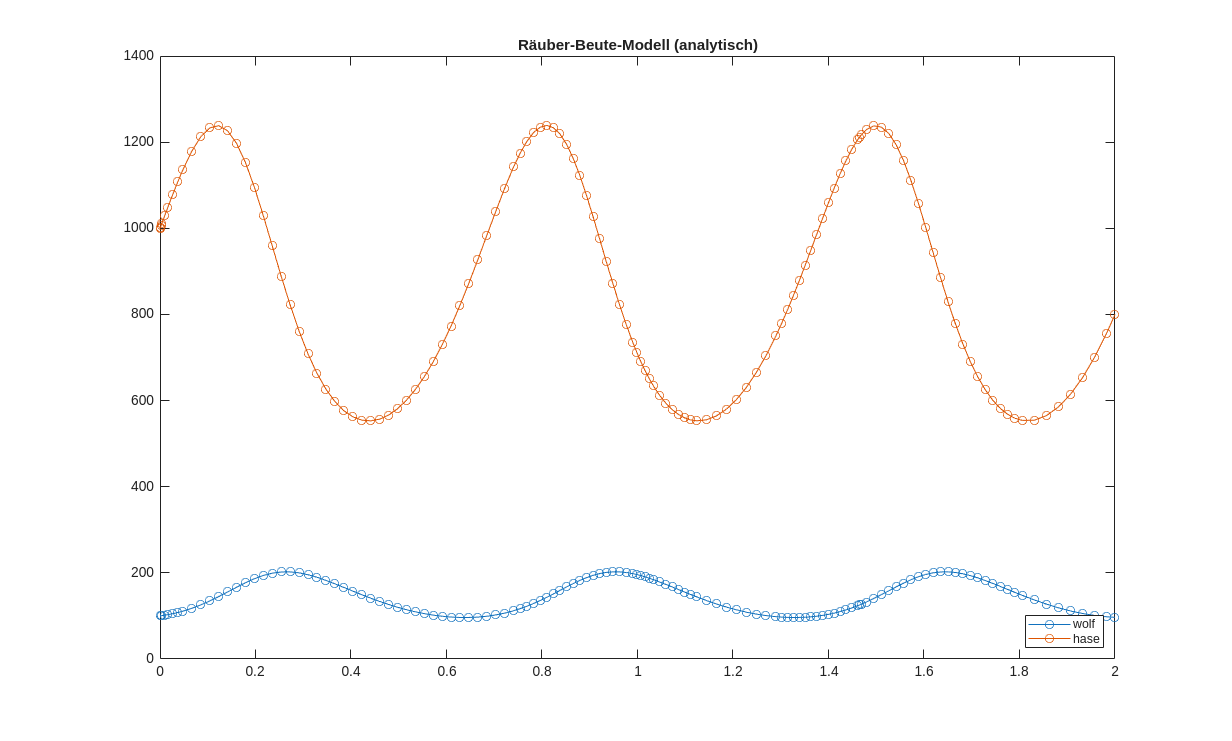
Und nochmal ODEs aber mit SensitivityF = ode;

p = [alpha, beta, gamma, delta];             % sensitivity variables
F = ode;
F.InitialValue = [wolf(1), hase(1)];
F.ODEFcn = @(t,y) [-p(1)*y(1)+p(3)*y(1)*y(2);
                    p(2)*y(2)-p(4)*y(2)*y(1) ];

F = ode(ODEFcn=@(t,y,p) [-p(1)*y(1)+p(3)*y(1)*y(2); p(2)*y(2)-p(4)*y(2)*y(1)], ...
        InitialValue=[wolf(1), hase(1)], ...
        Parameters=p, ...
        Sensitivity=odeSensitivity)

S=solve(F,0,tend);
plot(S.Time,S.Solution,"-o")
title('Räuber-Beute-Modell (analytisch)');
legend("wolf","hase",Location="southeast")

saveas(gcf,'wolf_hase_ode.jpg');

F = 

  ode with properties:

   <strong>Problem definition</strong>
               ODEFcn: [function_handle]
           Parameters: [8.5000 10 0.0100 0.0700]
          InitialTime: 0
         InitialValue: [100 1000]
          Sensitivity: [1×1 odeSensitivity]
         EquationType: standard

   <strong>Solver properties</strong>
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: auto
       SelectedSolver: cvodesnonstiff

  Show <a href="matlab:if exist('F','var'), ode.displayAll('F',F,'ode'); else, ode.displayAll('F'), end">all properties</a>

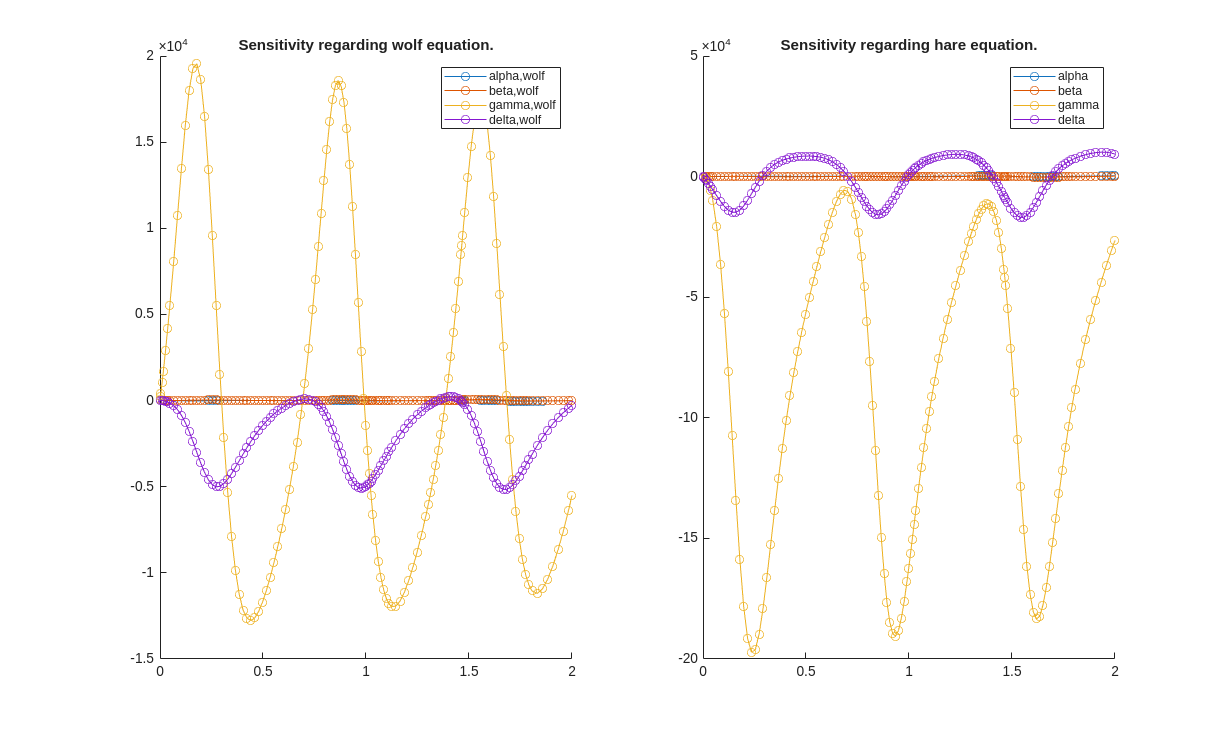
jetzt die Sensitivity

figure(3)
subplot(1,2,1)
hold on
plot(S.Time,squeeze(S.Sensitivity(1,1,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(1,2,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(1,3,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(1,4,:)),"-o")
legend("alpha,wolf","beta,wolf","gamma,wolf","delta,wolf")
title("Sensitivity regarding wolf equation.")
hold off

subplot(1,2,2)
hold on
plot(S.Time,squeeze(S.Sensitivity(2,1,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(2,2,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(2,3,:)),"-o")
plot(S.Time,squeeze(S.Sensitivity(2,4,:)),"-o")
legend("alpha","beta","gamma","delta")
title("Sensitivity regarding hare equation.")
hold off

Published with MATLAB® R2025b