Contents
- CompMath-Vorlesung 06.10.2023
- Symbolische Ausdruecke
- Symbolische Funktionen
- Manipulation algebraischer Ausdruecke
- Ausdrücke vereinfachen
- Algebraische Gleichungen
- Loese nach der einzigen Variablen auf: symbolisch
- Loese symbolisch mit Zusatzannahme
- Loese nach einer bestimmten Variablen symbolisch auf ("Umstellen nach")
- Schraenke das Loesen auf x>0 ein.
- Loese nach der einzigen Variablen auf: numerisch mit vpasolve()
- Loese nach der einzigen Variablen auf: numerisch fzero()
- Algebraische Gleichungssysteme
- Lineares System
- Variante 1: symbolisch (mit Parameter) via solve()
- Variante 2: numerisch via \
- Nichtlineares System
- Variante 1: symbolisch via solve()
- Grafics für obiges nichlineares Gleichungssystem
- nochmal symbolisch, aber mit Parameter in Loesung via solve()
- numerische Loesung via vpasolve()
- numerische Loesung via fsolve() [benoetigt die Optimization Toolbox]
- Integrieren und Differenzieren nach einer Variablen
- Int+Diff+Vereinfachen
- Integrieren und Differenzieren mehrdimensionaler Funktionen
- Gradient, Laplace, Rotation, Divergenz
- Grenzwerte:
- Evaluate the sum of the following multivariable expression with respect to k:
- Grafik mit symbolischen Funktionen
- Visualisierung mit 2 Variablen (nur mit Funktion moeglich)
CompMath-Vorlesung 06.10.2023
Demonstration symbolischer Methoden in Matlab, Siehe auch die gute Einfuehrung dazu.
close all; clear; clc % Präambel für Octave isOctave = exist('OCTAVE_VERSION', 'builtin') ~= 0; if (isOctave) pkg load symbolic % nur fuer octave noetig end
Symbolische Ausdruecke
clear disp('Symbolische Ausdruecke'); % Deklaration syms a b c; % deklariere symbolische Variablen f = 3*(a-1)*(b^2+c^3)*(exp(a+b)-1) % symbolischer Ausdrücke % Ersetzen von Variablen durch Zahlenwerten oder Ausdruecke subs(f, a, 3) % Ersetze a durch 3 subs(f, a, b) % Ersetze a durch (bereits als symb. def.) Variable b subs(f, a, 'x') % Ersetze a durch (noch nicht als symb.) Variable x subs(f, a, (b+c)^2) % Ersetze a durch den Term (b+c)^2 subs(f, [a,b,c], [-1,2,3]) % Ersetze die Variablen durch die Werte/Terme
Symbolische Ausdruecke f = (3*a - 3)*(b^2 + c^3)*(exp(a + b) - 1) ans = 6*(exp(b + 3) - 1)*(b^2 + c^3) ans = (3*b - 3)*(exp(2*b) - 1)*(b^2 + c^3) ans = (3*x - 3)*(b^2 + c^3)*(exp(b + x) - 1) ans = (exp(b + (b + c)^2) - 1)*(3*(b + c)^2 - 3)*(b^2 + c^3) ans = 186 - 186*exp(1)
Symbolische Funktionen
clear all; disp('Symbolische Funktionen'); % Deklaration syms a b c; % deklariere symbolische Variablen f(a,b,c) = 3*(a-1)*(b^2+c^3)*(exp(a+b)-1) % symbolische Funktion % Ersetzen von Variablen durch Zahlenwerten oder Ausdruecke f(3,b,c) % Ersetze a durch 3 f(b,b,c) % Ersetze a durch (bereits als symb. def.) Variable b f('x',b,c) % Ersetze a durch (noch nicht als symb.) Variable x f((b+c)^2,b,c) % Ersetze a durch den Term (b+c)^2 f(-1,2,3) % Ersetze die Variablen [a,b,c] durch die Werte/Terme
Symbolische Funktionen f(a, b, c) = (3*a - 3)*(b^2 + c^3)*(exp(a + b) - 1) ans = 6*(exp(b + 3) - 1)*(b^2 + c^3) ans = (3*b - 3)*(exp(2*b) - 1)*(b^2 + c^3) ans = (3*x - 3)*(b^2 + c^3)*(exp(b + x) - 1) ans = (exp(b + (b + c)^2) - 1)*(3*(b + c)^2 - 3)*(b^2 + c^3) ans = 186 - 186*exp(1)
Manipulation algebraischer Ausdruecke
a^2-2*a*b+b^2
clear; %clc; disp('Manipulation algebraischer Ausdruecke'); syms a b; % deklariere symb. Variablen f = a^2-2*a*b+b^2 % symb. Ausdruck fe = factor(f) % Faktoren bestimmen prod(fe) % ausmultiplizieren der Faktoren
Manipulation algebraischer Ausdruecke f = a^2 - 2*a*b + b^2 fe = [a - b, a - b] ans = (a - b)^2
Ausdrücke vereinfachen
disp('simple anwenden') ff=simplify(f) % (bestmoeglich) vereinfachen, zeigt alle Versuche expand(ff) % ausmultiplizieren der Ausdrücke
simple anwenden ff = (a - b)^2 ans = a^2 - 2*a*b + b^2
Algebraische Gleichungen
Loese x^2=16
Loese nach der einzigen Variablen auf: symbolisch
clear; %clc; disp('Loese nach der einzigen Variablen auf') % Loese x^2=16: Variante 1 syms x assume(x,'clear') % ensure that all old assumtions are deleted solve(x^2 == 16) % Loese x^2=16: Variante 2 syms x; y = x^2-16; solve(y==0, x) % Loest y(x) = 0
Loese nach der einzigen Variablen auf ans = -4 4 ans = -4 4
Loese symbolisch mit Zusatzannahme
clear; syms x assume(x,'clear') % ensure that all old assumtions are deleted f(x) = x^4 - x^3 - 5*x^2 - 7*x - 84 disp('Loese ohne Zusatzannahme') xsol = solve(f==0) disp('x soll reell sein') assume(x,'real') xsol = solve(f==0) disp('x soll zusaetzlich negativ sein') assumeAlso(x<0) xsol = solve(f==0) disp('assumptions(x) :') assumptions(x)
f(x) =
x^4 - x^3 - 5*x^2 - 7*x - 84
Loese ohne Zusatzannahme
xsol =
-3
4
-7^(1/2)*1i
7^(1/2)*1i
x soll reell sein
xsol =
-3
4
x soll zusaetzlich negativ sein
xsol =
-3
assumptions(x) :
ans =
[in(x, 'real'), x < 0]
Loese nach einer bestimmten Variablen symbolisch auf ("Umstellen nach")
Stelle y = 2*x^2+4 nach x um
clear; %clc; disp('Loese nach einer bestimmten Variablen auf') syms x y; f(x,y) = 2*x^2+4-y % Notwendig: f(x,y) = 0 % f(x) = sin(x)-x/2-0.1; aa = solve(f==0,x) pretty(aa) % Schoenere Ausgabe
Loese nach einer bestimmten Variablen auf f(x, y) = 2*x^2 - y + 4 aa = -(2^(1/2)*(y - 4)^(1/2))/2 (2^(1/2)*(y - 4)^(1/2))/2 / sqrt(2) sqrt(y - 4) \ | - ------------------- | | 2 | | | | sqrt(2) sqrt(y - 4) | | ------------------- | \ 2 /
Schraenke das Loesen auf x>0 ein.
assume(x>0) % nur positive Lösungen a1 = solve(f==0,x) % matlab weist auf Lösungsbedingung hin assume(4<y) % Lösungsbedingung bzgl. y festlegen a2 = solve(f==0,x)
Warning: Solutions are only valid under certain conditions. To include parameters and conditions in the solution, specify the 'ReturnConditions' value as 'true'. a1 = (2^(1/2)*(y - 4)^(1/2))/2 a2 = (2^(1/2)*(y - 4)^(1/2))/2
Loese nach der einzigen Variablen auf: numerisch mit vpasolve()
syms x; y = x^2-16; % y = sin(x)-x/2-0.1; disp('Numerisch mit vpasolve():') x0 = -1; % % sol = vpasolve(y) % funktioniert auch sol = vpasolve(y, x0) disp(['Startloesung ', num2str(x0), ' ergibt Lösung: ']); sol
Numerisch mit vpasolve(): sol = -4.0 4.0 Startloesung -1 ergibt Lösung: sol = -4.0 4.0
Loese nach der einzigen Variablen auf: numerisch fzero()
syms x; y = x^2-16; disp('Numerisch mit fzero():') x0 = -1; % %y_hand = @(x)subs(y,x); % Functionshandle aus symbolischer Fkt. erzeugen (alt) y_hand = matlabFunction(y); % numerische Funktion <-- symbolische Funktion sol = fzero(y_hand, x0) disp(['Loesung ',num2str(sol),' bei Startloesung ', num2str(x0)]);
Numerisch mit fzero():
sol =
-4
Loesung -4 bei Startloesung -1
Algebraische Gleichungssysteme
Lineares System
a + b = 3
a + 2*b = 6Variante 1: symbolisch (mit Parameter) via solve()
via f_1(a,b) := a + b - 3 = 0
f_2(a,b) := a + 2*b - c = 0clear; %clc; disp('Lineares System Variante 1: symbolisch') syms a b c; f(1) = a + b - 3; f(2) = a + 2*b - c; % f: vector of symbolic expressions [A,B] = solve(f,[a,b]) % 2 symb. Variable als Ergebnis % bzw SOLUTION = solve(f,[a,b]) % Cell Array als Ergebnis SOLUTION.a SOLUTION.b
Lineares System Variante 1: symbolisch
A =
6 - c
B =
c - 3
SOLUTION =
struct with fields:
a: 6 - c
b: c - 3
ans =
6 - c
ans =
c - 3
Variante 2: numerisch via \
via loesen von K*x = f (x entspricht [a b] aus symbolischer Loesung)
clear; %clc; disp('Lineares System Variante 2: numerisch') K = [1 1; 1 2]; % Koeffizientenmatrix f = [ 3; 6]; % rechte Seite x = K\f % Loesen des linearen Gleichungssystems
Lineares System Variante 2: numerisch
x =
0
3
Nichtlineares System
3a^2 + b^2 = 1
a + b = 1Variante 1: symbolisch via solve()
f_1(a,b) := 3a^2 + b^2 - 1 = 0
f_2(a,b) := a + b - 1 = 0clear; disp('Nichtlineares System Variante 1: symbolisch ') syms a b; ell(a,b) = 3*a^2 + b^2 - 1; line(a,b) = a + b - 1; f = [ ell, line ] % f: symbolic function [A,B] = solve(f) % bzw SOLUTION = solve(f) SOLUTION.a % beide Loesungen werden ausgegeben SOLUTION.b % Eine einzelne Loesung extrahieren Solution = [SOLUTION.a, SOLUTION.b] Solution1 = Solution(1,:)
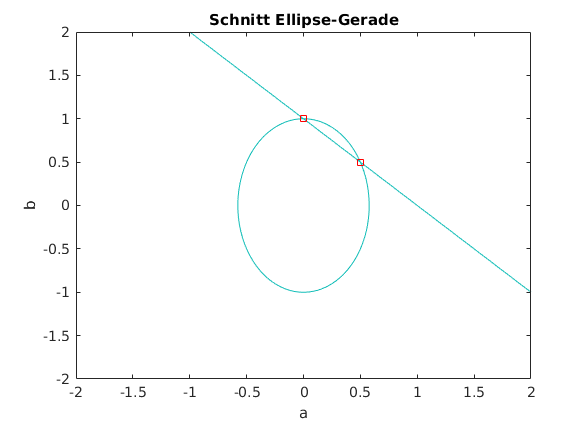
Nichtlineares System Variante 1: symbolisch
f(a, b) =
[3*a^2 + b^2 - 1, a + b - 1]
A =
0
1/2
B =
1
1/2
SOLUTION =
struct with fields:
a: [2×1 sym]
b: [2×1 sym]
ans =
0
1/2
ans =
1
1/2
Solution =
[ 0, 1]
[1/2, 1/2]
Solution1 =
[0, 1]
Grafics für obiges nichlineares Gleichungssystem
limits = [-2,2, -2,2]; % passende Grenzen für x,y wählen ezplot(ell,limits) % Ellipse hold on % zeichne weiter in die Grafik ezplot(line,limits) % Gerade plot(SOLUTION.a,SOLUTION.b, 'sr') % Zeichne die Schnittpunkte ein title("Schnitt Ellipse-Gerade") hold off % Grafik darf überschrieben werden
nochmal symbolisch, aber mit Parameter in Loesung via solve()
3a^2 + b^2 = c
a + b = c^2disp('Nichtlineares System Variante 1: symbolisch mit Variablen in Loesung') syms a b c d; f = [ 3*a^2 + b^2 - c, a + b - c^2 ]; % f: vector of symbolic expressions [A,B] = solve(f,a,b)
Nichtlineares System Variante 1: symbolisch mit Variablen in Loesung A = (-(c*(3*c^3 - 4))/4)^(1/2)/2 + c^2/4 c^2/4 - (-(c*(3*c^3 - 4))/4)^(1/2)/2 B = (3*c^2)/4 - (-(c*(3*c^3 - 4))/4)^(1/2)/2 (-(c*(3*c^3 - 4))/4)^(1/2)/2 + (3*c^2)/4
numerische Loesung via vpasolve()
3a^2 + b^2 = 1
a + b = 1disp('Nichtlineares System Variante 2: numerisch vpnsolve()') syms a b; f = [ 3*a^2 + b^2-1 , a + b-1]; % keine Leerzeichen vor '-1', da vpasolve() ansonsten Probleme hat x_0 = [0.3, 0.6]; sol = vpasolve(f, [a,b]) % auch vpasolve(f, [a,b], x_0) möglich % sol = vpasolve([3*a^2 + b^2-1, a+b-1], [a,b]) % disp(['Numerische Loesung bei Startloesung ',num2str(x_0)]) disp(['Numerische Loesung:']) sol.a sol.b
Nichtlineares System Variante 2: numerisch vpnsolve()
sol =
struct with fields:
a: [2×1 sym]
b: [2×1 sym]
Numerische Loesung:
ans =
0
0.5
ans =
1.0
0.5
numerische Loesung via fsolve() [benoetigt die Optimization Toolbox]
3a^2 + b^2 = 1
a + b = 1disp('Nichtlineares System Variante 3: numerisch fsolve') x_0 = [0.3, 0.6]; sol = fsolve(@(x)[3*x(1)^2 + x(2)^2 - 1; x(1) + x(2) - 1], x_0) disp(['Numerische Loesung ',num2str(sol),' bei Startloesung ',num2str(x_0)])
Nichtlineares System Variante 3: numerisch fsolve
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.
sol =
0.5000 0.5000
Numerische Loesung 0.5 0.5 bei Startloesung 0.3 0.6
Integrieren und Differenzieren nach einer Variablen
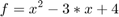
clear; %clc; disp('Integrieren und Differenzieren nach einer Variablen') syms x; f(x) = x^2 - 3*x + 4 % Differenzieren diff(f) % oder diff('x^2 - 3*x + 4') % Integrieren int(f) % unbestimmtes Integral int(f,x) int(f,0,1) % bestimmtes Integral int(f,x,0,1)
Integrieren und Differenzieren nach einer Variablen f(x) = x^2 - 3*x + 4 ans(x) = 2*x - 3 ans(x) = (x*(2*x^2 - 9*x + 24))/6 ans(x) = (x*(2*x^2 - 9*x + 24))/6 ans = 17/6 ans = 17/6
Int+Diff+Vereinfachen
syms x f(x) = exp(x)*cos(x) F = int(f,x) Fx = diff(F,x) Fx-f % das soll == 0 sein? simplify(Fx-f) % OK, jetzt glaube ich das.
f(x) = exp(x)*cos(x) F(x) = (exp(x)*(cos(x) + sin(x)))/2 Fx(x) = (exp(x)*(cos(x) + sin(x)))/2 + (exp(x)*(cos(x) - sin(x)))/2 ans(x) = (exp(x)*(cos(x) + sin(x)))/2 - exp(x)*cos(x) + (exp(x)*(cos(x) - sin(x)))/2 ans(x) = 0
Integrieren und Differenzieren mehrdimensionaler Funktionen
![$$f = [a^2 + b^2 - 1, a + b - 1]$$](v_1_a_eq01233701879853513526.png)
clear; %clc; disp('Integrieren und Differenzieren mehrdimensionaler Funktionen') syms a b f = [a^2 + b^2 - 1, a + b - 1] Jac = jacobian(f); f1_a = diff(f(1),a) % 1. Ableitung 1. Funktion bzgl. a f1_a = diff(f(1),2) % 2. Ableitung 1. Funktion bzgl. a int(f(1)) % unbestimmtes Integral bzgl. letzer Variable int(f(1),a) % unbestimmtes Integral bzgl. Variable a int(f(1),a,1,2) % bestimmtes Integral bzgl. Variable a
Integrieren und Differenzieren mehrdimensionaler Funktionen f = [a^2 + b^2 - 1, a + b - 1] f1_a = 2*a f1_a = 2 ans = b^3/3 + b*(a^2 - 1) ans = a^3/3 + a*(b^2 - 1) ans = b^2 + 4/3
Gradient, Laplace, Rotation, Divergenz
clear %clc syms x y z a f(x,y,z) = x^3+sin(y)^2+exp(a*z) % Gradient von f disp('Gradient von f') gradient(f,[x,y,z]) % Laplace von f disp('Laplace von f') laplacian(f,[x,y,z]) % Divergenz von g g(x,y,z) = [x^3+sin(y)^2+exp(a*z); exp(x)-log(z); y*z+x*y] disp('Divergenz von g') divergence(g,[x,y,z]) % Rotation von g disp('Rotation von g') curl(g,[x,y,z])
f(x, y, z) =
x^3 + sin(y)^2 + exp(a*z)
Gradient von f
ans(x, y, z) =
3*x^2
2*cos(y)*sin(y)
a*exp(a*z)
Laplace von f
ans(x, y, z) =
6*x + 2*cos(y)^2 - 2*sin(y)^2 + a^2*exp(a*z)
g(x, y, z) =
x^3 + sin(y)^2 + exp(a*z)
exp(x) - log(z)
x*y + y*z
Divergenz von g
ans(x, y, z) =
3*x^2 + y
Rotation von g
ans(x, y, z) =
x + z + 1/z
a*exp(a*z) - y
exp(x) - 2*cos(y)*sin(y)
Grenzwerte:
from docu for limit : 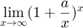
syms x a; pretty(limit((1 + a/x)^x, x, inf))
exp(a)
Evaluate the sum of the following multivariable expression with respect to k:
from docu for 'symsum'
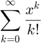
syms x k; pretty(symsum(x^k/factorial(k), k, 0, inf)) % anderes Bsp: $ \sum_{k=1}^\infty \frac{1}{k^2} $ pretty(symsum(1/k^2, k, 1, inf))
exp(x) 2 pi --- 6
Grafik mit symbolischen Funktionen
clear, clf syms x real %assume(x,'real') g(x) = (x+x*cos(x))/(2*exp(x)-log(x)); % Symb. Funktion interval = [0,10]; ezplot(g ,interval); %fplot(g ,interval) g1 = diff(g,x); % 1. Ableitung hold on ezplot(g1 ,interval); %fplot(g1 ,interval) g2 = diff(g,2,x); % 2. Ableitung ezplot(g2 ,interval); %fplot(g2 ,interval) legend("g(x)","g'(x)","g''(x)") % Beschriftung der Plots % Convert <https://de.mathworks.com/help/symbolic/sym.latex.html symbolic function to latex-string> ss = ['$g(x)=',latex(g(x)),'$']; title(['Demonstration 1D: ',ss],'interpreter','latex'); % title("Demonstration 1D Funktion") saveas(gcf,'g_1d.jpg') % Speichere aktuelle Grafik in File hold off
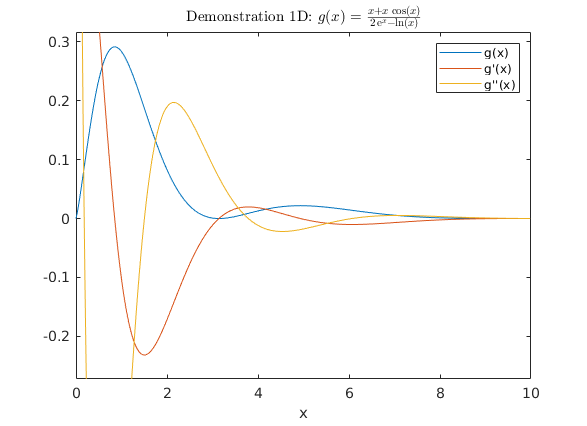
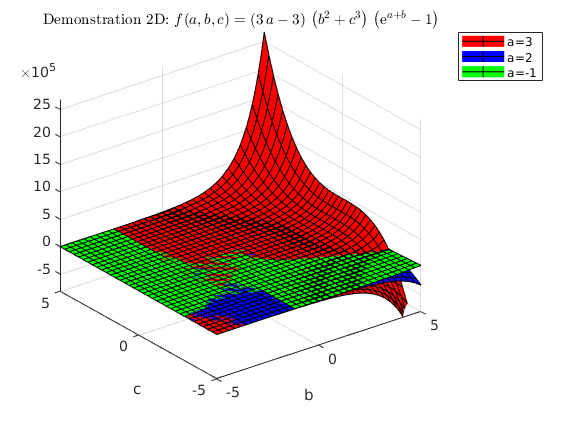
Visualisierung mit 2 Variablen (nur mit Funktion moeglich)
figure() % 2. Grafikfenster syms a b c; % deklariere symbolische Variablen f(a,b,c) = 3*(a-1)*(b^2+c^3)*(exp(a+b)-1) % symbolische Funktion % Präambel für Octave if (exist('OCTAVE_VERSION', 'builtin') == 0) % Matlab branch fsurf( f(3,b,c)); % Flaeche g(b,c) % kombininierte Grafik fuer mehrere Werte von 'a' hold off % vorherige Grafik wird überschrieben fsurf( f(3,b,c),'r') % Flaeche g_3(b,c) in 'red' (--> LineSpec) xlabel('b'); ylabel('c'); % Achsenbeschriftung hold on % fuege die naechsten Plots zur Grafik hinzu fsurf( f(2,b,c),'b'); % Flaeche g_2(b,c) in 'blue' fsurf( f(-1,b,c),'g'); % Flaeche g_1(b,c) in 'green' legend('a=3','a=2','a=-1') % Beschriftung der Plots ss = ['$f(a,b,c)=',latex(f(a,b,c)),'$']; title(['Demonstration 2D: ',ss],'interpreter','latex'); % title("Demonstration 2D-Funktion") saveas(gcf,'f_2d.jpg') % Speichere aktuelle Grafik in File hold off % Grafik wird von nächstem Plot ueberschrieben else % Octave branch ezsurf( f(3,b,c)); % Flaeche g(b,c) % kombininierte Grafik fuer mehrere Werte von 'a' hold off % vorherige Grafik wird überschrieben ezsurf( f(3,b,c)) % Flaeche g_3(b,c) in 'red' (--> LineSpec) xlabel('b'); ylabel('c'); % Achsenbeschriftung hold on % fuege die naechsten Plots zur Grafik hinzu ezsurf( f(2,b,c)); % Flaeche g_2(b,c) in 'blue' ezsurf( f(-1,b,c)); % Flaeche g_1(b,c) in 'green' legend('a=3','a=2','a=-1') % Beschriftung der Plots title("Demonstration 2D-Funktion") saveas(gcf,'f_2d.jpg') % Speichere aktuelle Grafik in File hold off end
f(a, b, c) = (3*a - 3)*(b^2 + c^3)*(exp(a + b) - 1)
Publishing publish('v_1_a.m')