Contents
Inkugel eines Tetraeders
clear, clc, close all
Punkte des Tetraeders
% a = [ 0 0 0 ]; b = [ 2 0 0 ]; c = [ 0 1 0 ]; d = [ 0 0 4 ]; % spezielle Lage a = [ 9 -1 2 ]; b = [ 1 3 4 ]; c = [ -1 4 2 ]; d = [ 1 0 1 ]; % allg. %
Normalenvektoren der 4 Tetraederflächen
Rechtsregel beachten (Normalenvektoren sollen nach Innen zeigen) Kann zum Bsp durch Einsetzen des Tetraederschwerpunktes S in die Formel d = N x (S -X) erzielt werden. Falls d<0, dann ist N = -N notwendig.
n1 = cross( b-a, c-a ); % und n1 = n1/norm(n1); % normalisieren n2 = cross( d-a, b-a ); % und n2 = n2/norm(n2); % normalisieren n3 = cross( c-a, d-a ); % und n3 = n3/norm(n3); % normalisieren n4 = cross( b-c, d-c ); % und n4 = n4/norm(n4); % normalisieren %
Herleitung und Definition of Matrix A and rechter Seite f des Gleichungssystems
zur Berechnung des Inkreismittelpunktes M und dessen Radius r Lösungsvektor u = [ M_x M_y M_z r]'
Herleitung der ersten Matrixzeile aus dem normierten Normalevektor n1 und Pkt. A:
Sei alpha = Winkel DMA (D ist unbekannter Lotpunkt auf Dreiecksflaeche) und Radius r=|D-M| :
rechtwinkliges Dreieck ADM ==> r = |M-A|*cos(alpha) (1) Skalarprodukt ==> < M-A, n1> = |n1|*|M-A|*cos(alpha) (2) Aus (1),(2) folgt wegen |n1|=1: r = < M-A, n1> <==> <M,n1> - r = <A,n1> was einer Gleichung mit 4 Unbekannten (M_x,M_y,M_z,r) entspricht. Analog fuer B,C,D mit n2,n3,m4 entsprechend und es entsteht nachfolgendes GlS.
% Gleichunssystem, aufstellen A = [ n1(1) n1(2) n1(3) -1; n2(1) n2(2) n2(3) -1; n3(1) n3(2) n3(3) -1; n4(1) n4(2) n4(3) -1; ]; f = [ dot(n1,a); dot(n2,a); dot(n3,a); dot(n4,d) ]; % und das Gleichungsystem lösen u = A\f; %
Ergebnisausgabe
M = u(1:3); % die ersten 3 Komponenten der Loesung des GlS Radius = u(4); % die 4. Komponenten der Loesung des GlS disp(' '); disp('Koordinaten der 4 Eckpunkte des Tetraeders') disp(vertcat(a,b,c,d)) disp(' '); disp(['Inkreismittelpunkt: ', num2str(M')]) %disp(M) disp(' '); disp(['Radius: ',num2str(Radius)]) %disp(Radius)
Koordinaten der 4 Eckpunkte des Tetraeders
9 -1 2
1 3 4
-1 4 2
1 0 1
Inkreismittelpunkt: 1.2966 2.1889 2.4117
Radius: 0.59281
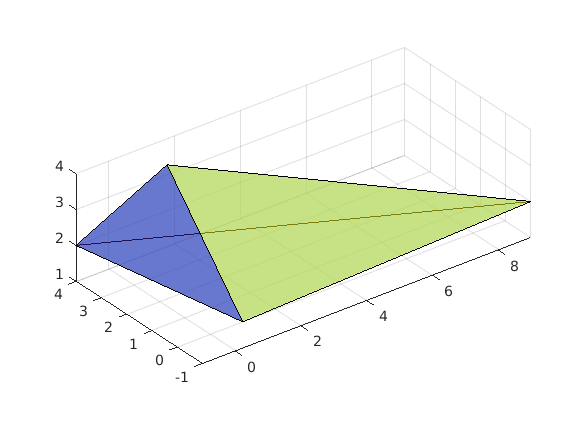
Tetraeder visualisieren
Koordinaten
koord = horzcat(a', b', c', d'); tri = [ 1 2 3; 1 2 4; 1 3 4; 2 3 4]; % Eckpunkte der 4 Dreiecksflaechen trisurf(tri, koord(1,:), koord(2,:), koord(3,:) ) alpha(.5) % transparency factor axis equal hold
Current plot held
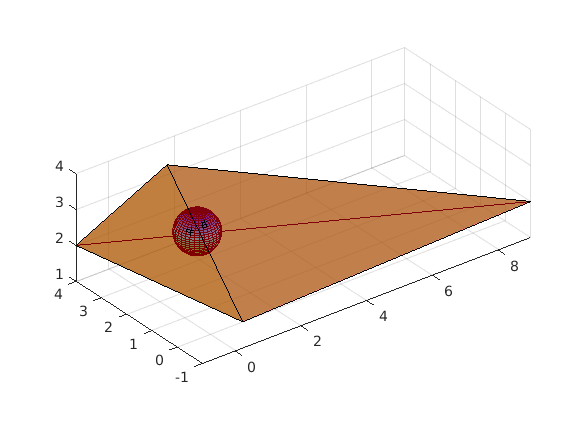
Kugel visualisieren
n = 2^5-1; ellipsoid(M(1),M(2),M(3),Radius,Radius,Radius,n) colormap hsv; axis equal %publish('InkugelTetraeder.m')